畳み込みは多倍長演算や画像/音声処理などによく使われる有名な演算で、特に離散値での演算は最近のマルチメディアといわれる分野では目に見えない形で利用されている。 例えば、デジカメを使う時のオートフォーカス、ボケ補正などといった画像処理や、ホール/ルーム/ゲームエフェクトでの音声処理ではしばしば使われている。 SONYの「AV/Hifiオーディオ コンポーネント 総合カタログ」(抜粋[PDF])にあるDCフェーズリニアライザーやCinema Studio EXはすべて畳み込みである FIRで実装するのが一番高速な方法である。ちなみにCinema Studio EXは10秒以上の畳み込みをしているようだ。
畳み込みは時間領域では通常O(n^2)のアルゴリズムなので、周波数領域にDFTで変換して積和演算単体ではO(n)で済ますことが多い。DFTでの変換自体は複素数のおかげで 演算量が減るのでO(nlogn)で済み、トータルでも時間領域の演算より速くなる。DFTなどのアルゴリズムはFFTW3などで実装されているので 詳しくはそちらを参照するとわかりやすいと思われる。
DFT後の周波数領域での畳み込みは、複素数の乗算となり、(a+bi)*(c+di)のループとなる。ここではまず(a+bi)*(c+di)のループの最適化を考えてみる。 普通に複素数の乗算だから、(ac-bd)+(ad+bc)iを求めればよい。
ここで利用するFFTW3は、実数数列のDFTが複素共役対称であり高速化できることからHalfcomplex-format DFTという演算方法を持っており、利用方法としては順方向は
float *in, *out;
in = fftwf_malloc(sizeof(float)*size);
out = fftwf_malloc(sizeof(float)*size);
fftwf_plan p;
p = fftwf_plan_r2r_1d(size, in, out, FFTW_R2HC, FFTW_ESTIMATE);
fftwf_execute(p);
fftwf_destroy_plan(p);
fftwf_free(in);
fftwf_free(out);
// 以下malloc/freeは省略
逆方向は
fftwf_plan p;
p = fftwf_plan_r2r_1d(size, in, out, FFTW_HC2R, FFTW_ESTIMATE);
fftwf_execute(p);
fftwf_destroy_plan(p);
のようになり、結果の配列には
r0, r1, r2, ..., rn/2, i(n+1)/2-1, ..., i2, i1
のように格納されており、これを複素数演算するとすると、以下のようなコードを実行することになる。
out[0] = x[0] * y[0]; // r0
out[n/2] = x[n/2] * y[n/2]; // r(n/2)
for (j = 1; j < n/2; j++)
{
float a = x[j];
float b = x[n - j];
float c = y[j];
float d = y[n - j];
out[j] += a*c-b*d; // Re
out[n - j] += a*d+b*c; // Im
}
まず、このコードの問題点として、順方向と逆方向との二つの方向の読み込みが存在するため、最適化できないことがあげられる。そこで、まず、データの配列を変換することから考える。以下のように配列を変換する。
out[0] = orig[0];
out[1] = orig[n/2];
for(int t = 1;t < n/2;t ++)
{
out[2*t+0] = orig[t];
out[2*t+1] = orig[n-t];
}
すると、データ構造は以下のようになる。
r0, rn/2, r1, i1, r2, i2, ..., r(n+1)/2-1, i(n+1)/2-1
このデータ構造を利用するコードは以下のようになる。
out[0] = x[0] * y[0]; // r0
out[1] = x[1] * y[1]; // r(n/2)
for (j = 1; j < n/2; j++)
{
float a = x[j*2];
float b = x[j*2+1];
float c = y[j*2];
float d = y[j*2+1];
out[j*2] += a*c-b*d; // Re
out[j*2+1] += a*d+b*c; // Im
}
これでいくらかは速くなる。しかし、これはスカラ計算の場合であって、もしベクトル化しようとなるとさらに話は発展する。どのようにデータ構造をとれば一番高速な計算ができるかということだ。
IntelやAMDでは、最適化に関する情報をかなりの量提供しており、参考になるが、その中の「インターネット・ストリーミング SIMD拡張命令を考慮したアプリケーション・チューニング」というarticleでは、AoS(Arrays-of-Structure)やSoA(Structure-of-Arrays)という言葉で説明している。要は配列の構造が構造単位か要素単位かということである。 もちろん、Aosを利用して、計算前に転置すればよいともいえる。 (参考:AMD64 アーキテクチャ技術資料、 Intel 日本語技術資料のダウンロード)
struct
{
float A[1000], B[1000], C[1000];
} SoA_data;
struct
{
float A, B, C;
} AoS_data[1000];
結論からいうと、3DNow!、SSEの場合は以下のようなデータ構造が好ましい。
struct
{
float Re[2], Im[2]; // 16 byte
} Complex_SoA_3DNOW[N/2];
struct
{
float Re[4]; // 16byte alignment for movaps
float Im[4]; // 16byte alignment for movaps
} Complex_SoA_SSE[N/4];
これらのデータ構造を作るには、以下のようなコードを利用すればよい。ただし最初は例外である。
// 3DNow!
// sizeof(out[] = orig[])
out[0] = orig[0]; // r0
out[1] = orig[1]; // r1
out[2] = orig[n/2]; // r(n/2)
out[3] = orig[n-1]; // i1
for(int t = 1;t < n/4;t ++)
{
out[4*t+0] = orig[2*t];
out[4*t+1] = orig[2*t+1];
out[4*t+2] = orig[n-2*t];
out[4*t+3] = orig[n-2*t-1];
}
// SSE
// sizeof(out[] = orig[])
out[0] = orig[0]; // r0
out[1] = orig[1]; // r1
out[2] = orig[2]; // r2
out[3] = orig[3]; // r3
out[4+0] = orig[n/2]; // r(n/2)
out[4+1] = orig[n-1]; // i1
out[4+2] = orig[n-2]; // i2
out[4+3] = orig[n-3]; // i3
for(int t = 1;t < n/8;t ++)
{
out[8*t+0] = orig[4*t];
out[8*t+1] = orig[4*t+1];
out[8*t+2] = orig[4*t+2];
out[8*t+3] = orig[4*t+3];
out[8*t+4+0] = orig[n-4*t];
out[8*t+4+1] = orig[n-4*t-1];
out[8*t+4+2] = orig[n-4*t-2];
out[8*t+4+3] = orig[n-4*t-3];
}
これで準備は整った。3DNow!の場合、2並列、SSEの場合、4並列で乗算、加算、減算を行うことができる。イメージは以下のようになる。ちなみに、movapsは16byte alignmentを要求するので、FFTW3のmallocを利用するとよい。
# source,dest
# 3DNow!
femms
for(...){
movq x.Re, mm0 # mm0 = a
movq mm0, mm2 # mm2 = a
movq y.Re, mm1 # mm1 = c
pfmul mm1, mm0 # mm0 = a*c
movq x.Im, mm4 # mm4 = b
movq mm4, mm3 # mm3 = b
pfmul mm1, mm3 # mm3 = b*c
movq y.Im, mm5 # mm5 = d
pfmul mm5, mm2 # mm2 = a*d
pfmul mm5, mm4 # mm4 = b*d
pfsub mm4, mm0 # mm0 = a*c - b*d
pfadd out.Re, mm0 # mm0 = Re + a*c - b*d
movq mm0, out.Re # Re = Re + a*c - b*d
pfadd mm3, mm2 # mm2 = a*d - b*c
pfadd out.Im, mm2 # mm2 = Im + a*d - b*c
movq mm2, out.Im # Im = Im + a*d - b*c
}
femms
# SSE
for(...){
movaps x.Re, xmm0 # xmm0 = a
movaps xmm0, xmm2 # xmm2 = a
movaps y.Re, xmm1 # xmm1 = c
mulps xmm1, xmm0 # xmm0 = a*c
movaps x.Im, xmm4 # xmm4 = b
movaps xmm4, xmm3 # xmm3 = b
mulps xmm1, xmm3 # xmm3 = b*c
movaps y.Im, xmm5 # xmm5 = d
mulps xmm5, xmm2 # xmm2 = a*d
mulps xmm5, xmm4 # xmm4 = b*d
subps xmm4, xmm0 # xmm0 = a*c - b*d
addps out.Re, xmm0 # xmm0 = Re + a*c - b*d
movaps xmm0, out.Re # Re = Re + a*c - b*d
addps xmm3, xmm2 # xmm2 = a*d - b*c
addps out.Im, xmm2 # xmm2 = Im + a*d - b*c
movaps xmm2, out.Im # Im = Im + a*d - b*c
}
ところで、3DNow!/SSE化するメリットは、勿論高速化であるが、本当にその意味があるのかといった点でプロファイラを利用する価値がある。いくつかのページで、SSE化 したのにあまり速くならなかったという記述を見かけるが、これは、SSEのPentium自体での実装がしょぼいという他に、同時実行/依存関係といった様々な問題をかかえているためで、 本当にどこを最適化すればよいか絞るためにもプロファイラの利用をおすすめする。 GNUには、gprofが存在し、gccでは-pgを付加することでプロファイル情報をgmon.outに出力するプログラムを生成するようになる。gmon.outのあるディレクトリ でgprof (バイナリ名)とするとだいたいの場合情報を表示してくれる(出力テキスト)。以下はその抜粋である。ちなみに使用プログラムは、 Freeverb3のsamples/impulse3である。(最適化前)
% cumulative self self total
time seconds seconds calls ms/call ms/call name
69.36 3.60 3.60 165698 0.02 0.02 frag::processMULT(float*, float*, float*, float*)
5.39 3.88 0.28 20272 0.01 0.02 frag::processR2HC(float*, float*, float*, float*)
4.24 4.10 0.22 10579 0.02 0.02 frag::processHC2R(float*, float*, float*, float*)
3.47 4.28 0.18 62934 0.00 0.00 irmodel3::mute(float*, int)
3.28 4.45 0.17 9973 0.02 0.47 irmodel3::processZL(float*, float*, float*, float*, long, unsigned int)
2.89 4.60 0.15 20602 0.01 0.01 blockDelay::push(float*)
2.89 4.75 0.15 9696 0.02 0.51 irmodel3::processreplace(float*, float*, float*, float*, long, unsigned int)
2.12 4.86 0.11 19854354 0.00 0.00 delay::process(float)
1.73 4.95 0.09 40742 0.00 0.00 frag::mute(float*, int)
1.73 5.04 0.09 9419 0.01 0.01 splitLR(float*, float*, float*, int)
1.35 5.11 0.07 9697 0.01 0.01 dump(void*, int)
0.58 5.14 0.03 main
fragmentSize = 1024
wetDB = 0.000000
factor = 16
loadImpulse(sample = 282953,FFTW_ESTIMATE)...done.
*** irmodel3 config ***
impulseSize = 282953
short Fragment Size = 1024
large Fragment Size = 16384
short Fragment vector Size = 16
large Fragment vector Size = 17
00002b17/00002b18
Wait for IR...
00000114/00000115
real 0m16.655s
user 0m16.293s
sys 0m0.208s
ここからもわかるように複素数乗算にかなりの時間がかかっていることがわかる。もしベクトル化によって2倍の速さになればかなりの改善を期待できることになるが、それはアセンブラの書き方/プリフェッチの仕方にかかっている。
次にアセンブラを使用する準備をする。もちろん、Cのみで開発しているのであればアセンブラ単体で使用することもできるが、C++を使っているとなると名前規則などで 困難を伴うので、インラインアセンブラを使うのがよいことになる。VC++などに関してはドキュメントが豊富であるし、Portabilityという面からここではGCCでの インラインアセンブラを利用することにする。基本的には以下のように使用する。
#include <stdio.h>
int main ()
{
float a[2] = {1.0, 2.0};
float b = 4.0;
float c[2];
/* a/b の低精度推定値を計算する。(正確な結果はc={0.25,0.5})*/
/*
一つ目の入力値には配列 a のアドレス &a を使い、そのアドレスにある
メモリ内容を movq で %mm0 に移動する。二つ目の入力値は変数 b を使
い、movd で %mm1 に移動する。
まず %mm1 の逆数をとり、それを %mm0 に掛ける。
結果は出力用の配列 c に割り当てたレジスタ %0 に movq で移動する。
*/
__asm__ __volatile__ ("movq (%1),%%mm0 \n\t"
"movd %2,%%mm1 \n\t"
"pfrcp %%mm1,%%mm1 \n\t"
"pfmul %%mm1,%%mm0 \n\t"
"movq %%mm0,%0 \n\t"
"femms \n\t"
: "=g" (c)
: "r" (&a), "r" (b)
:);
printf ("c={%g,%g}\n", c[0], c[1]);
return 0;
}
上の例は3DNow!の使用の例である。まず、アセンブラのセクションは基本的に__asm__ __volatile__ ("アセンブラのコード":出力:入力:破壊レジスタ);である。 入力や出力で%0などを利用する場合はレジスタを%でなく%%で修飾するようにする。asmやvolatileのようにアンダーバーを入れなくてもよいが、予約されていることがあるので、なるべくアンダーバーで 囲むようにする。これだけではわかりにくいので、もう少し詳しく説明すると、アセンブラのコードはその直前に入力のコードが、その直後に出力のコードが追加される。 入出力の時に=gやrといったようにレジスタを指定するが、その時に破壊レジスタは避けられて自動的に割り当てられる。上のCのアセンブラのコードは以下のようになっている。 objdump -S (バイナリ名)でソースコード混合でアセンブラのソースを参照できる。
float a[2] = {1.0, 2.0};
8048445: b8 00 00 80 3f mov $0x3f800000,%eax
804844a: 89 45 f0 mov %eax,0xfffffff0(%ebp)
804844d: b8 00 00 00 40 mov $0x40000000,%eax
8048452: 89 45 f4 mov %eax,0xfffffff4(%ebp)
float b = 4.0;
8048455: b8 00 00 80 40 mov $0x40800000,%eax
804845a: 89 45 f8 mov %eax,0xfffffff8(%ebp)
float c[2];
asm volatile (...)
804845d: 8d 55 f0 lea 0xfffffff0(%ebp),%edx
8048460: 8b 45 f8 mov 0xfffffff8(%ebp),%eax
8048463: 0f 6f 02 movq (%edx),%mm0
8048466: 0f 6e c8 movd %eax,%mm1
8048469: 0f 0f c9 96 pfrcp %mm1,%mm1
804846d: 0f 0f c1 b4 pfmul %mm1,%mm0
8048471: 0f 7f 45 e8 movq %mm0,0xffffffe8(%ebp)
8048475: 0f 0e femms
printf ("c={%g,%g}\n", c[0], c[1]);
8048477: d9 45 ec flds 0xffffffec(%ebp)
804847a: d9 45 e8 flds 0xffffffe8(%ebp)
804847d: d9 c9 fxch %st(1)
804847f: 83 ec 0c sub $0xc,%esp
8048482: 8d 64 24 f8 lea 0xfffffff8(%esp),%esp
8048486: dd 1c 24 fstpl (%esp)
8048489: 8d 64 24 f8 lea 0xfffffff8(%esp),%esp
804848d: dd 1c 24 fstpl (%esp)
8048490: 68 88 85 04 08 push $0x8048588
8048495: e8 d6 fe ff ff call 8048370 <printf@plt>
804849a: 83 c4 20 add $0x20,%esp
まず、
804845d: 8d 55 f0 lea 0xfffffff0(%ebp),%edx
8048460: 8b 45 f8 mov 0xfffffff8(%ebp),%eax
に注目する。これは、asmブロック内の直前のコードであり、
: "r" (&a), "r" (b)
から生成されている。&aはポインタであり、そのアドレスを示すleaがrつまりeax,ebx,ecx,edx,esi,ediの中から自動割り当てされてedxに格納されている。 次に、bはそのままeaxに格納されている。これでアセンブラコードブロック内で変数を利用することができるようになった。ブロック内では%1や%2という形で 書いているが、それらがそれぞれedxやeaxとなっていることがわかるだろう。ちなみに、"r"などの文字についてはConstraints for 'asm' Operandsを参照するとよい (Constraints - Using the GNU Compiler Collection (GCC))。 高速化したいなどの希望があれば、0x??(%ebp)といったスタック上でなくレジスタ上にマップされるようにqやrを使用すればよい。ただ、x86はレジスタの数が少ないので、 入力部分であまりqを使い過ぎたり、破壊レジスタに多くのレジスタを指定すると、以下のようなエラーを吐くことになる。
: "q"(oL), "q"(iL), "q"(fL), "q"(size)
: "eax", "ebx");
とやると明らかに配分するレジスタの数が足りないので
(oL,iL,fL,sizeはeax,ebxを除いたecx,edxのみでは割り当てられない。
qはeax,ebx,ecx,edxを示すConstraintsである。)
mul2.cpp:20: error: can't find a register in class 'Q_REGS' while reloading 'asm'
とかエラーになる。
/tmp/cc5TY99c.s:49: Error: suffix or operands invalid for `movq'
また、最適化などをするとしばしばinlineなどを行なったりするために様々な問題が起こる事があり、本当に理解するまでは-O0でインラインアセンブラを使った方が 良いかもしれない。そして、きちんとアセンブラをかいた時点で初めてコンパイラの方の最適化をかけるとよい。ただし、ジャンプラベルを使っている場合はinlineを -fno-inline-functionsで抑制しないと
/tmp/ccFb9zvd.s:230: Error: symbol `mul3_3dnow__' is already defined
といったエラーになる。これは勿論、inlineによって同一コード内に同一ラベルが生じることによる。まずは試すのが良い。以下は GCCでインラインアセンブリを使用する方法と留意点等 for x86からの抜粋である。
| "a" | eax |
| "b" | ebx |
| "c" | ecx |
| "d" | edx |
| "s" | esi |
| "D" | edi |
| "I" | 0〜31までの定数 for 32 bit shifts |
| "J" | 0〜63までの定数 for 64 bit shifts |
| "K" | 定数0xff |
| "L" | 定数0xffff |
| "M" | 0,1,2,3のうちの定数 (shifts for `lea') |
| "N" | 0〜255までの定数 (`out'命令向け) |
| "G" | 80387標準浮動小数点定数 |
| "q" | 自動割り当て(eax,ebx,ecx,edxの中から) |
| "r" | 自動割り当て(eax,ebx,ecx,edx,esi,ediの中から) |
| "g" | eax,ebx,ecx,edx もしくは許される凡ゆるアドレスのメモリ |
| "m" | 許される凡ゆるアドレスのメモリ |
| "A" | eaxとedxを合わせて64bitのlong long型で使う。 |
| "f" | 数値浮動小数点レジスタの中から自動割り当て |
| "t" | 浮動小数点スタックの先頭の数値浮動小数点レジスタ |
| "u" | 浮動小数点スタックの2番目の数値浮動小数点レジスタ |
| "0","1","2",... | 入出力オペランド部分で割り当てられたレジスタやメモリを割り当てられた順に指す。 |
| = | 書き込み専用を意味し、以前の値を消して、asm文の アセンブリ部分で書き込まれた値を持つようにする。 |
| + | 読み書き両用を意味する。 |
| & | そのオペランドが、入力オペランドの使用が終わる前に 破損することに対して適切に対処する。 すなわち、そのオペランドをインプット用のレジスタや メモリから切り離すことで、入力オペランドが壊れたレ ジスタに影響されることを防ぐ。 |
86系で浮動小数点を扱う際は、入力用に"f"を1つでも使うならば、 出力オペランドに "=f"ではなく、"=&t" など、 "&"付のものを使う必要がある。 また、出力用のオペランドはスタックの先頭、つまり "=&t" から始めなければならない。そうしなければ、まともな動作は保証されない。
次に、出力についてであるが、アセンブラブロックでは%0にmovqで書き込んでいる。この
"movq %%mm0,%0 \n\t"
が実際のコードでは
8048471: 0f 7f 45 e8 movq %mm0,0xffffffe8(%ebp)
となっており、正しく書き込みされていることがわかる。これである程度準備できたので、今度はベクトル演算をしてみる。以下にスカラ演算と3DNow!を利用したベクトル演算の例を示す。
#include <stdio.h>
// oL[] = iL[] * fL[]
void mulScalar(float * iL, float * fL, float * oL, int size)
{
for(int i = 0;i < size;i ++)
oL[i] = iL[i] * fL[i];
return;
}
void mulVector(float * iL, float * fL, float * oL, int size)
{
size /= 2;
__asm__ __volatile__ ("femms");
__asm__ __volatile__ ("mul3_3dnow__: \n\t"
"movq (%1), %%mm0 \n\t"
"movq (%2), %%mm1 \n\t"
"pfmul %%mm1, %%mm0 \n\t"
"movq %%mm0, (%0) \n\t"
"add $0x8, %0 \n\t"
"add $0x8, %1 \n\t"
"add $0x8, %2 \n\t"
"dec %3 \n\t"
"jnz mul3_3dnow__"
:
: "q"(oL), "q"(iL), "q"(fL), "q"(size)
:);
__asm__ __volatile__ ("femms");
return;
}
int main(int argc, char **argv)
{
static int N = 4096;
float * fL = new float[N];
float * iL = new float[N];
float * oL = new float[N];
fL[0] = 0.1f; fL[1] = 0.2f; iL[0] = 0.4f; iL[1] = 0.9f;
fL[N-2] = 0.1f; fL[N-1] = 0.2f; iL[N-2] = 0.3f; iL[N-1] = 0.2f;
mulScalar(fL, iL, oL, N);
fprintf(stderr, "[0,1] %f %f\n", oL[0], oL[1], oL[2], oL[3]);
fprintf(stderr, "[N-2,N-1] %f %f\n", oL[N-2], oL[N-1]);
mulVector(fL, iL, oL, N);
fprintf(stderr, "[0,1] %f %f\n", oL[0], oL[1], oL[2], oL[3]);
fprintf(stderr, "[N-2,N-1] %f %f\n", oL[N-2], oL[N-1]);
delete[] fL;
delete[] iL;
delete[] oL;
}
出力は以下の通りどちらも同じである。
[0,1] 0.040000 0.180000
[N-2,N-1] 0.030000 0.040000
[0,1] 0.040000 0.180000
[N-2,N-1] 0.030000 0.040000
RDTSCを使ってSMPだと不正確ながらクロックを計ってみる。以下のクロックはAMD Athlon(tm) 64 X2 Dual Core Processor 4600+を使用したものである。
#include <stdio.h>
inline long long rdtsc()
{
long long tsc;
__asm__ __volatile__ ("rdtsc":"=A" (tsc));
return tsc;
}
void mulScalar(float * iL, float * fL, float * oL, int size)
{
for(int i = 0;i < size;i ++)
oL[i] = iL[i] * fL[i];
return;
}
void mulVector(float * iL, float * fL, float * oL, int size)
{
size /= 2;
__asm__ __volatile__ ("femms");
__asm__ __volatile__ ("mul3_3dnow__: \n\t"
"movq (%1), %%mm0 \n\t"
"movq (%2), %%mm1 \n\t"
"pfmul %%mm1, %%mm0 \n\t"
"movq %%mm0, (%0) \n\t"
"add $0x8, %0 \n\t"
"add $0x8, %1 \n\t"
"add $0x8, %2 \n\t"
"dec %3 \n\t"
"jnz mul3_3dnow__"
:
: "q"(oL), "q"(iL), "q"(fL), "q"(size)
:);
__asm__ __volatile__ ("femms");
return;
}
int main(int argc, char **argv)
{
long long tsc_start, tsc_stop, tsc_min;
static int N = 4*4096;
static int C = 10;
float * fL = new float[N];
float * iL = new float[N];
float * oL = new float[N];
fprintf(stderr, "%d bytes allocated.\n", 3*sizeof(float)*N);
fL[0] = 0.1f; fL[1] = 0.2f; iL[0] = 0.4f; iL[1] = 0.9f;
fL[N-2] = 0.1f; fL[N-1] = 0.2f; iL[N-2] = 0.3f; iL[N-1] = 0.2f;
for(int i = 0;i < C;i ++)
{
tsc_start = rdtsc();
mulScalar(fL, iL, oL, N);
tsc_stop = rdtsc();
if(i == 0)
tsc_min = tsc_stop - tsc_start;
else
if(tsc_min > tsc_stop - tsc_start)
tsc_min = tsc_stop - tsc_start;
}
fprintf(stderr, "Scalar Clock: %ld\n", tsc_min/N);
for(int i = 0;i < C;i ++)
{
tsc_start = rdtsc();
mulVector(fL, iL, oL, N);
tsc_stop = rdtsc();
if(i == 0)
tsc_min = tsc_stop - tsc_start;
else
if(tsc_min > tsc_stop - tsc_start)
tsc_min = tsc_stop - tsc_start;
}
fprintf(stderr, "Vector Clock: %ld\n", tsc_min/(N/2));
delete[] fL;
delete[] iL;
delete[] oL;
}
とりあえずクロックのおおよその最小値は以下のようになった。
196608 bytes allocated.
Scalar Clock: 8
Vector Clock: 15
ここから考えられる遅い原因は、浮動小数点演算といっても実行ユニットは同じであること、加算と乗算を同時実行できるわけでもないこと、 おそらくベクトル演算では克服できないメモリバンド/レイテンシなどの壁があることなどである。
ここでレイテンシを調べてみる。 Software Optimization Guide for AMD64 Processorsの Appendix C Instruction Latenciesを参照すると、以下の抜粋のようになっている。
ADD mreg16/32/64, imm16/32 81h 11-000-xxx DirectPath 1
ADD mem16/32/64, imm16/32 81h mm-000-xxx DirectPath 4
ADD mreg16/32/64, imm8 (sign extended) 83h 11-000-xxx DirectPath 1
ADD mem16/32/64, imm8 (sign extended) 83h mm-000-xxx DirectPath 4
DEC mem16/32/64 FFh mm-001-xxx DirectPath 4
DEC mreg16/32/64 FFh 11-001-xxx DirectPath 1
JNE/JNZ disp8 75h DirectPath 1 *1
JNE/JNZ disp16/32 0Fh 85h DirectPath 1 *1
MOVQ mmreg1, mmreg2 0Fh 6Fh 11-xxx-xxx DirectPath FADD/FMUL 2
MOVQ mmreg, mem64 0Fh 6Fh mm-xxx-xxx DirectPath FADD/FMUL/FSTORE 4 *2
MOVQ mmreg2, mmreg1 0Fh 7Fh 11-xxx-xxx DirectPath FADD/FMUL 2
MOVQ mem64, mmreg 0Fh 7Fh mm-xxx-xxx DirectPath FSTORE 2
PFMUL mmreg1, mmreg2 0Fh, 0Fh B4h 11-xxx-xxx DirectPath FMUL 4
PFMUL mmreg, mem64 0Fh, 0Fh B4h mm-xxx-xxx DirectPath FMUL 6
*1. Static timing assumes a predicted branch.
*2. These instructions have an effective latency as shown.
However, these instructions generate an internal NOP
with a latency of two cycles but no related dependencies.
These internal NOPs can be executed at a rate of
three per cycle and can use any of the three execution resources.
ここから考えると、かなりレイテンシがかさんでいることがわかる。ちなみに以下のループのみでは3クロックである。inc,cmp,jneすべてが依存しているのですべて実行して3クロックとなるのだろう。
__asm__ __volatile__ ("mul3_3dnow__: \n\t"
"inc %%eax \n\t"
"cmp %%eax, %3 \n\t"
"jne mul3_3dnow__"
そこでプリフェッチの登場である。以下のようにprefetchを挿入してみる。
__asm__ __volatile__ ("mul3_3dnow__: \n\t"
"prefetch 0xプリフェッチ先のアドレス(%1) \n\t"
"movq (%1), %%mm0 \n\t"
プリフェッチするアドレスを試すとそれぞれ以下のようになる。
prefetchなし
Scalar Clock: 8
Vector Clock: 15
+0x0
Scalar Clock: 8
Vector Clock: 16
+0x10
Scalar Clock: 8
Vector Clock: 15
+0x20
Scalar Clock: 8
Vector Clock: 11
+0x40
Scalar Clock: 8
Vector Clock: 11
+0x80
Scalar Clock: 8
Vector Clock: 10
+0x100
Scalar Clock: 8
Vector Clock: 10
+0x120
Scalar Clock: 8
Vector Clock: 9
+0x140
Scalar Clock: 8
Vector Clock: 9
+0x200
Scalar Clock: 8
Vector Clock: 10
+0x1000
Scalar Clock: 8
Vector Clock: 20
prefetch 0x120(%1)近辺が一番効果が高く、ループあたり9クロックですんでいることがわかる。命令数が9なので、だいぶ良くなった。ちなみに以下のように レジスタ数を減らすことで見やすくなるし、もしかしたら速くなるかもしれない。
__asm__ __volatile__ ("xor %%eax, %%eax \n\t"
"mul3_3dnow__: \n\t"
"prefetch 0x120(%1,%%eax,8) \n\t"
"movq (%1,%%eax,8), %%mm0 \n\t"
"movq (%2,%%eax,8), %%mm1 \n\t"
"pfmul %%mm1, %%mm0 \n\t"
"movq %%mm0, (%0,%%eax,8) \n\t"
"inc %%eax \n\t"
"cmp %%eax, %3 \n\t"
"jne mul3_3dnow__"
ただ少なくとも雑な言い方をすれば、x87 FPUに比べて3DNow!は文字どおり倍速になったわけだ。しかしこれにはかなり誤りが含まれている。まず、このプログラムで allocateされているメモリのサイズに注意する。196608 bytes allocated.と表示されているとおり、現在使用しているCPUの二次キャッシュにおさまるサイズのデータを 計算している。そこでデータサイズを変化させてみると以下のようになる。
size Scalar Vector Vector w/o PF
12288 2 4 4
24576 2 4 4
49152 3 4 4
98304 14 16 16
196608 14 16 16
393216 10 17 16
786432 13 19 22
1572864 13 19 22
3145728 14 19 22
6291456 14 20 22
Athlon64X2の一次データキャッシュ(L1)が64KiBであることから、49152byteまでは非常に速い演算ができているとがわかり、prefetchがL1に読み込む命令であること を考えると、w/o PreFecthとの差があまりない理由がわかる。AMD Athlon X2 Dual-Core Processor Product Data Sheetによれば、
64-Kbyte 2-Way Associative ECC-Protected L1 Data Caches
Two 64-bit operations per cycle, 3-cycle latency
なので、L1は1クロックあたり最高2x64bitのデータを読み書きでき、今回の場合、ループ/L1読み書きが同時に実行されて高速に動いていることになる。
また、二次キャッシュが512KiBなのでそれを超えるとクロックは上がる。サイズが大きくなってくるとプリフェッチの効果が見えてくる。ただし、最近のCPUはハードウエアプリフェッチを行うので その効果があまり見えないという問題はある。
ここでメモリバスの幅を考える。今回使用しているのはDDR 800 (PC2-6400) dual channelなので6.4x2=12.8GB/秒である。 CPUは2.4Gなので、CPUクロックあたり最高16/3byteの転送ができる。但しこれはシーケンシャルな読み込みの場合である。また、Hammer-Infoによれば
130nmでも90nmでもL2 Latencyは12 cyclesであったが、Brisbaneでは20 cyclesである。
AMDの回答によると、将来的にキャッシュサイズを増やすことも可能なように
意図的にLatencyを増やしたのだという。
ということで、現在使用中なのは90nm製品なのでL2からの読み込みには最低12クロックかかるとみてよいだろう。すると、先程述べたようにループ3クロック、 ベクトル演算1クロック、キャッシュからの読み込みで12クロックとなり、サイズがL1を越えたあたりで16クロックとなると思われる。以上から、すでにキャッシュやメモリの 読み書きの速度の壁のせいでベクトル演算が思ったように速くは動いていないということが推測できる。実際は計算はもっと複雑なので、もし計算内容がメモリ読み込みよりも 時間がかかるならばSIMD化する価値があるといえる。計算内容よりもメモリ読み込みの方が時間がかかるようになると、ストールが発生する。 最終的には以下のような最適化コードを考えた。二次キャッシュの範囲ではいくらか速くなったが、それでもメインメモリの領域になると最適化は難しい。 データがくるまでクロックを消費して待っているのだろう。
__asm__ __volatile__ ("xor %%eax, %%eax \n\t"
"mul3_3dnow__: \n\t"
"prefetch 0x120(%2,%%eax,8) \n\t"
"movq (%1,%%eax,8), %%mm0 \n\t"
"pfmul (%2,%%eax,8), %%mm0 \n\t"
"movq %%mm0, (%0,%%eax,8) \n\t"
"inc %%eax \n\t"
"cmp %%eax, %3 \n\t"
"jne mul3_3dnow__"
:
: "q"(oL), "q"(iL), "q"(fL), "r"(size)
: "eax");
size Scalar Vector Vector w/o PF
12288 2 4 4
24576 2 4 4
49152 3 4 4
98304 14 14 13
196608 14 14 14
393216 10 14 18
786432 13 17 22
1572864 13 19 22
3145728 14 19 23
6291456 14 19 23
さて、複素数乗算の本題に戻る。以下のように、スカラ、スカラ2回、3DNow!ベクトル演算を利用した場合のクロックをはかる。
#include <stdio.h>
inline long long rdtsc()
{
long long tsc;
__asm__ __volatile__ ("rdtsc":"=A" (tsc));
return tsc;
}
void complexScalar(float * x, float * y, float * out, int n)
{
for (int j = 0; j < n/2; j++)
{
float a = x[j*2];
float b = x[j*2+1];
float c = y[j*2];
float d = y[j*2+1];
out[j*2] += a*c-b*d; // Re
out[j*2+1] += a*d+b*c; // Im
}
}
void complexScalar2(float * iL, float * fL, float * oL, int size)
{
for(int i = 0;i < (size/4);i ++)
{
// Re
oL[4*i+0] += iL[4*i+0]*fL[4*i+0]-iL[4*i+2]*fL[4*i+2];
oL[4*i+1] += iL[4*i+1]*fL[4*i+1]-iL[4*i+3]*fL[4*i+3];
// Im
oL[4*i+2] += iL[4*i+0]*fL[4*i+2]+iL[4*i+2]*fL[4*i+0];
oL[4*i+3] += iL[4*i+1]*fL[4*i+3]+iL[4*i+3]*fL[4*i+1];
}
}
void complex3DNOW(float * iL, float * fL, float * oL, int size)
{
size /= 4;
__asm__ __volatile__ ("femms");
__asm__ __volatile__ ("mul_3dnow__: \n\t"
"movq (%1), %%mm0 \n\t"
"movq %%mm0, %%mm2 \n\t"
"movq (%2), %%mm1 \n\t"
"pfmul %%mm1, %%mm0 \n\t"
"movq 0x8(%1), %%mm4 \n\t"
"movq %%mm4, %%mm3 \n\t"
"pfmul %%mm1, %%mm3 \n\t"
"movq 0x8(%2), %%mm5 \n\t"
"pfmul %%mm5, %%mm2 \n\t"
"pfmul %%mm5, %%mm4 \n\t"
"pfsub %%mm4, %%mm0 \n\t"
"pfadd (%0), %%mm0 \n\t"
"movq %%mm0, (%0) \n\t"
"pfadd %%mm3, %%mm2 \n\t"
"pfadd 0x8(%0), %%mm2 \n\t"
"movq %%mm2, 0x8(%0) \n\t"
"add $0x10, %0 \n\t"
"add $0x10, %1 \n\t"
"add $0x10, %2 \n\t"
"dec %3 \n\t"
"jne mul_3dnow__"
:
: "q"(oL), "q"(iL), "q"(fL), "q"(size)
:);
__asm__ __volatile__ ("femms");
}
void work(int N, int C)
{
long long tsc_start, tsc_stop, tsc_min;
float * fL = new float[N];
float * iL = new float[N];
float * oL = new float[N];
fprintf(stderr, "%d\t", 3*sizeof(float)*N);
for(int i = 0;i < C;i ++)
{
tsc_start = rdtsc();
complexScalar(fL, iL, oL, N);
tsc_stop = rdtsc();
if(i == 0)
tsc_min = tsc_stop - tsc_start;
else
if(tsc_min > tsc_stop - tsc_start)
tsc_min = tsc_stop - tsc_start;
}
fprintf(stderr, "%ld\t", tsc_min/(N/2));
for(int i = 0;i < C;i ++)
{
tsc_start = rdtsc();
complex3DNOW(fL, iL, oL, N);
tsc_stop = rdtsc();
if(i == 0)
tsc_min = tsc_stop - tsc_start;
else
if(tsc_min > tsc_stop - tsc_start)
tsc_min = tsc_stop - tsc_start;
}
fprintf(stderr, "%ld\t", tsc_min/(N/4));
for(int i = 0;i < C;i ++)
{
tsc_start = rdtsc();
complexScalar2(fL, iL, oL, N);
tsc_stop = rdtsc();
if(i == 0)
tsc_min = tsc_stop - tsc_start;
else
if(tsc_min > tsc_stop - tsc_start)
tsc_min = tsc_stop - tsc_start;
}
fprintf(stderr, "%ld\n", tsc_min/(N/4));
delete[] fL;
delete[] iL;
delete[] oL;
}
int main(int argc, char **argv)
{
// static int N = 4*4096;
static int N = 4*256;
static int C = 30;
fprintf(stderr, "size\tScalar\t3DNow!\tScalar2\n");
for(int i = 0;i < 10;i ++)
{
work(N, C);
N *= 2;
}
}
size Scalar 3DNow! Scalar2
12288 11 10 23
24576 10 10 24
49152 10 10 26
98304 33 38 100
196608 37 43 103
393216 34 39 70
786432 48 50 110
1572864 49 51 111
3145728 49 52 112
6291456 50 52 112
ループあたりのクロックだから、ほぼ3DNow!は倍速であることになる。先程の単純な乗算の場合は計算内容が単純だったためにメモリバンドの 壁があったが、この場合は計算内容がある程度複雑なので、メモリバンドにあまり左右されずに高速化できたと考えられる。 ちなみに、Athlon thunderbird 800MHz (PC133)の場合、以下のようになり、3DNow!を利用しても性能が悪化していることから、 メインメモリのレイテンシがかなり影響していることがわかる。Opteron以降のAMDのメモリコントローラ内蔵CPUはメインメモリのレイテンシを削減したことで かなり性能を伸ばしたようだ。
size Scalar 3DNow! Scalar2
12288 11 11 23
24576 12 11 24
49152 10 10 25
98304 36 38 94
196608 38 46 96
393216 27 34 64
786432 43 55 108
1572864 52 81 123
3145728 51 81 124
6291456 51 82 124
次にSSEを利用してみる。movapsは16byte alignmentを要求するので少々複雑になる。
#include <stdio.h>
#include <fftw3.h>
inline long long rdtsc()
{
long long tsc;
__asm__ __volatile__ ("rdtsc":"=A" (tsc));
return tsc;
}
void complexSSE(float * iL, float * fL, float * oL, int count)
{
__asm__ __volatile__ ("mul_sse__: \n\t"
"movaps (%1), %%xmm0 \n\t"
"movaps %%xmm0, %%xmm2 \n\t"
"movaps (%2), %%xmm1 \n\t"
"mulps %%xmm1, %%xmm0 \n\t"
"movaps 0x10(%1), %%xmm4 \n\t"
"movaps %%xmm4, %%xmm3 \n\t"
"mulps %%xmm1, %%xmm3 \n\t"
"movaps 0x10(%2), %%xmm5 \n\t"
"mulps %%xmm5, %%xmm2 \n\t"
"mulps %%xmm5, %%xmm4 \n\t"
"subps %%xmm4, %%xmm0 \n\t"
"addps (%0), %%xmm0 \n\t"
"movaps %%xmm0, (%0) \n\t"
"addps %%xmm3, %%xmm2 \n\t"
"addps 0x10(%0), %%xmm2 \n\t"
"movaps %%xmm2, 0x10(%0) \n\t"
"add $0x20, %0 \n\t"
"add $0x20, %1 \n\t"
"add $0x20, %2 \n\t"
"dec %3 \n\t"
"jne mul_sse__"
:
: "q"(oL), "q"(iL), "q"(fL), "q"(count)
:);
}
void work(int N, int C)
{
long long tsc_start, tsc_stop, tsc_min;
float * fL = (float*)fftwf_malloc(sizeof(float)*N*2);
float * iL = (float*)fftwf_malloc(sizeof(float)*N*2);
float * oL = (float*)fftwf_malloc(sizeof(float)*N*2);
fprintf(stderr, "%d\t", 3*sizeof(float)*N*2);
for(int i = 0;i < C;i ++)
{
tsc_start = rdtsc();
complexSSE(fL, iL, oL, N/4);
tsc_stop = rdtsc();
if(i == 0)
tsc_min = tsc_stop - tsc_start;
else
if(tsc_min > tsc_stop - tsc_start)
tsc_min = tsc_stop - tsc_start;
}
fprintf(stderr, "%ld\n", tsc_min/(N/4));
fftwf_free(fL);
fftwf_free(iL);
fftwf_free(oL);
}
int main(int argc, char **argv)
{
// static int N = 4*4096;
static int N = 4*128;
static int C = 10;
fprintf(stderr, "size\tSSE\n");
for(int i = 0;i < 10;i ++)
{
work(N, C);
N *= 2;
}
}
ループあたりのクロックは以下の通りである。
size SSE
12288 18
24576 19
49152 19
98304 52
196608 55
393216 61
786432 95
1572864 97
3145728 98
6291456 99
4倍速は無理だが二次キャッシュの範囲のみでは2倍程度は高速化できそうである。しかし、メインメモリの領域では大幅な最適化は難しいと考えられる。
以上のことを利用して、Fragment Multiplier (class frag)をSIMD化し、SSEを利用した場合のsamples/impulse3のプロファイリング結果は以下のようになった。(抜粋)
% cumulative self self total
time seconds seconds calls ms/call ms/call name
69.81 2.92 2.92 multMONO_sse__
6.92 3.21 0.29 10013 0.03 0.10 irmodel3_f::processreplace(float*, float*, float*, float*, long, unsigned int)
5.73 3.46 0.24 10916 0.02 0.03 frag_f::processHC2R(float*, float*, float*, float*)
4.53 3.65 0.19 41918 0.00 0.00 frag_f::convertR2SIMD(float*, float*, int)
3.10 3.77 0.13 10014 0.01 0.01 dump(void*, int)
2.63 3.88 0.11 21832 0.01 0.01 frag_f::convertSIMD2R(float*, float*, int)
2.15 3.98 0.09 10290 0.01 0.06 irmodel3_f::processZL(float*, float*, float*, float*, long, unsigned int)
1.91 4.05 0.08 20503506 0.00 0.00 delay_f::process(float)
1.43 4.12 0.06 10013 0.01 0.01 mergeLR(float*, float*, float*, int)
0.95 4.16 0.04 9736 0.00 0.00 splitLR(float*, float*, float*, int)
0.24 4.17 0.01 171107 0.00 0.00 frag_f::processMULT(float*, float*, float*, float*)
0.24 4.17 0.01 20926 0.00 0.01 frag_f::processR2HC(float*, float*, float*, float*)
0.24 4.18 0.01 4 2.50 2.50 blockDelay_f::setBlock(int, int)
0.12 4.19 0.01 342214 0.00 0.00 frag_f::multMONO(float*, float*, float*, int)
fragmentSize = 1024
wetDB = 0.000000
factor = 16
loadImpulse(sample = 282953,FFTW_ESTIMATE)...done.
*** irmodel3 config ***
impulseSize = 282953
short Fragment Size = 1024
large Fragment Size = 16384
short Fragment vector Size = 16
large Fragment vector Size = 17
00002b17/00002b18
Wait for IR...
00000114/00000115
real 0m14.774s
user 0m14.609s
sys 0m0.168s
時間的には8/7倍程度速くなったが、データの並べかえに少し時間がかかっていることがわかる。このため、SSEにはデータシャッフル用の命令が用意されており、フレキシブルにデータ構造を利用できる。 ただ、今回の場合、上からわかるように並べかえを高速化してもほとんど速くならないだろうことが予測できる。 Athlon64X2の場合、浮動小数点演算であってもかなり速いので、メモリ帯域などの壁があってなかなか高速化することができない。
gprofなどのプロファイラを利用した場合、関数単位での時間はわかるが、命令毎での時間を知りたいという場合は、パフォーマンスカウンタを利用することになる。 パフォーマンスカウンタとは、最近のCPUには備わっているレジスタの一種で、キャッシュミスなどのパフォーマンスに関する統計を取るために利用できるものである。 これらはユーザーランドからは一部しか利用できないので、一般的にはカーネルモード(カーネルモジュールあるいはドライバ)を読み込んで利用することになる。 intelのVTuneや、GPLのoprofileやperfmon2などがそれにあたるが、 幸いなことに、Linux 2.6以降では標準でoprofileを利用することができる。そこで、ここではoprofileを利用してみたい。 カーネルのオプションでInstrumentation SupportまたはCONFIG_PROFILING,CONFIG_OPROFILE,CONFIG_KPROBESとして利用できる。まずはこれらを使用して カーネルを作りなおして起動する。opcontrol -lとすると以下のように利用できるカウンタが表示される。
oprofile: available events for CPU type "AMD64 processors"
CPU_CLK_UNHALTED: (counter: all)
Cycles outside of halt state (min count: 3000)
RETIRED_INSTRUCTIONS: (counter: all)
Retired instructions (includes exceptions, interrupts, re-syncs) (min count: 3000)
RETIRED_UOPS: (counter: all)
Retired micro-ops (min count: 500)
INSTRUCTION_CACHE_FETCHES: (counter: all)
Instruction cache fetches (RevE) (min count: 500)
INSTRUCTION_CACHE_MISSES: (counter: all)
Instruction cache misses (min count: 500)
DATA_CACHE_ACCESSES: (counter: all)
Data cache accesses (min count: 500)
DATA_CACHE_MISSES: (counter: all)
Data cache misses (min count: 500)
...以下略
まずは実際に利用してみる。opcontrol -sで開始するので、その後調べたいプログラムを起動する。終ったらopcontrol -tで終了する。 /var/lib/oprofile/samples/current/にカウンタの内容が記録される。まずopreportとすると、概要が表示される。
CPU: AMD64 processors, speed 2399.98 MHz (estimated)
Counted CPU_CLK_UNHALTED events (Cycles outside of halt state) \
with a unit mask of 0x00 (No unit mask) count 100000
CPU_CLK_UNHALT...|
samples| %|
------------------
467853 36.0132 libfftw3f.so.3.2.0
164017 12.6253 libfreeverb3.so.2.0.0
160743 12.3733 impulse3
158160 12.1744 libc-2.5.so
136565 10.5122 libfreeverb3.so.2.0.0
60555 4.6613 vmlinux
47917 3.6884 libsamplerate.so.0.1.1
...以下略
opgprof (バイナリ名)とするとgprofで読めるgmon.outを作成してくれる。この内容はほぼ-pgで作成できるものと同じであるが、パフォーマンスカウンタ の内容を指定して入れることもできる。それについては後述する。内容は以下のようなものである。
Flat profile:
Each sample counts as 1 samples.
% cumulative self self total
time samples samples calls T1/call T1/call name
34.88 107853.00 107853.00 multMONO_sse__
33.09 210189.00 102336.00 frag_f::allocFFT(int, unsigned int)
4.20 223177.00 12988.00 _init
3.39 233663.00 10486.00 irmodel3_f::irmodel3_f()
3.30 243875.00 10212.00 frag_f::processHC2R(float*, float*, float*, float*)
3.00 253146.00 9271.00 readSoundFloatLR(SNDFILE_tag*, SF_INFO*, float*, float*, int)
2.33 260359.00 7213.00 irmodel3_f::processZL(float*, float*, float*, float*, long, unsigned int)
2.26 267349.00 6990.00 dump(void*, int)
1.94 273359.00 6010.00 irmodel3_f::processreplace(float*, float*, float*, float*, long, unsigned int)
1.90 279245.00 5886.00 frag_f::convertR2SIMD(float*, float*, int)
1.52 283941.00 4696.00 delay_f::delay_f()
1.41 288316.00 4375.00 frag_f::convertSIMD2R(float*, float*, int)
...
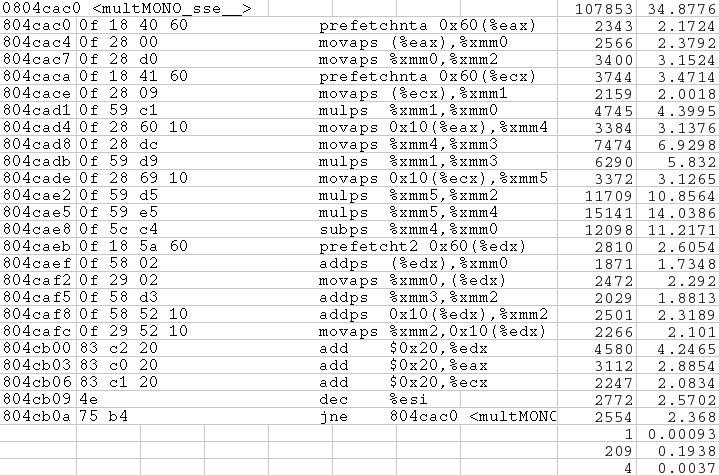
そして、命令毎の結果はopreport -d (バイナリ名)で表示できる。
CPU: AMD64 processors, speed 2399.98 MHz (estimated)
Counted CPU_CLK_UNHALTED events (Cycles outside of halt state) \
with a unit mask of 0x00 (No unit mask) count 100000
vma samples % symbol name
0804cac0 107853 34.8776 multMONO_sse__
0804cac0 2343 2.1724
0804cac4 2566 2.3792
0804cac7 3400 3.1524
0804caca 3744 3.4714
0804cace 2159 2.0018
0804cad1 4745 4.3995
0804cad4 3384 3.1376
0804cad8 7474 6.9298
0804cadb 6290 5.8320
0804cade 3372 3.1265
0804cae2 11709 10.8564
0804cae5 15141 14.0386
0804cae8 12098 11.2171
0804caeb 2810 2.6054
0804caef 1871 1.7348
0804caf2 2472 2.2920
0804caf5 2029 1.8813
0804caf8 2501 2.3189
0804cafc 2266 2.1010
0804cb00 4580 4.2465
0804cb03 3112 2.8854
0804cb06 2247 2.0834
0804cb09 2772 2.5702
0804cb0a 2554 2.3680
0804cb0c 1 9.3e-04
0804cb0d 209 0.1938
0804cb0e 4 0.0037
アセンブラのコードとマージすると以下のようになる。

以上だけ見ると、SIMDによる最適化が意味のないものに見えてくるので、やる気を出すために、非常に効果があるという例も示しておく。例えば、以下の環境では、以上のSSE最適化に非常に意味がある。
Pentium4 520 (2.8GHz,FSB 800MHz,1MB L2 Cache)
E7221 PC2-3200 DDR2-400 ECC 512M
Linux 2.6.24-gentoo-r8
Pentium3やPentium4はAthlon系に比べてx87 FPUが非常に遅いという話は有名だが、どれだけ違うかというと以下のとおり8倍くらい違う。(process t が畳み込みにかかった時間。)
Benchmark: freeverb3-2.3.0 fv3_benchmark
FPU
-=-=-=-=- Results -=-=-=-=-
irLength 480000 (10.00[s]@48kHz)
fragmentS 1024
factor 16
process t 1024000 (21.33[s]@48kHz)
load time 0.19[s] (x52.63@48kHz)
process t 5.92[s] (x3.60@48kHz)
SSE optimized
-=-=-=-=- Results -=-=-=-=-
irLength 480000 (10.00[s]@48kHz)
fragmentS 1024
factor 16
process t 1024000 (21.33[s]@48kHz)
load time 0.17[s] (x58.82@48kHz)
process t 0.85[s] (x25.10@48kHz)
ちなみにloadの時間はFFTW3に依存しているので、あまり差がついていない。プリフェッチ命令を多用したこともあるが、最適化が有効なこともあるのだ。 Core2Duo世代以降のIntelのCPUはこれほど差が出ることが少なくなったらしいが、それでもAthlon系のFPUの早さには特筆すべき物があると思う。ちなみに昔のAthlonでもそれなりの最適化の意味はあるようだ。
Athlon 800MHz
KT133A PC133 384M
FPU
-=-=-=-=- Results -=-=-=-=-
irLength 480000 (10.00[s]@48kHz)
fragmentS 1024
factor 16
process t 1024000 (21.33[s]@48kHz)
load time 0.67[s] (x14.93@48kHz)
process t 9.00[s] (x2.37@48kHz)
3DNow! optimized
-=-=-=-=- Results -=-=-=-=-
irLength 480000 (10.00[s]@48kHz)
fragmentS 1024
factor 16
process t 1024000 (21.33[s]@48kHz)
load time 0.66[s] (x15.15@48kHz)
process t 7.41[s] (x2.88@48kHz)
更に詳しいことは、SAXPYやZAXPYという言葉で探すことができる。
4. User Friendliness and Graphical User Interface:
Most people are not very user-friendly. Try talking to a person (especially of
the opposite sex) and trying to guess what you're supposed to do now, what the
other person wants from you, what would happen if you did this, and what would
happen if you did that, and how the heck to you get the other person to do
what you really want. No more of that! People should get a graphical user
interface. Why talk to the other person in that complex command line language
we call "Hebrew", when you can just look at the menu, see the options "Leave
me alone" and "Let's have sex" and just chose the one you want! Better yet,
why not have a toolbar, with nice little icons?
-- Nadav Har'El
-- Hackers-IL Message No. 1,408 ( http://tech.groups.yahoo.com/group/hackers-il/message/1408 )
Q: What lies on the bottom of the ocean and twitches?
A: A nervous wreck.