[ Main Page ]

R について Octaveとの比較

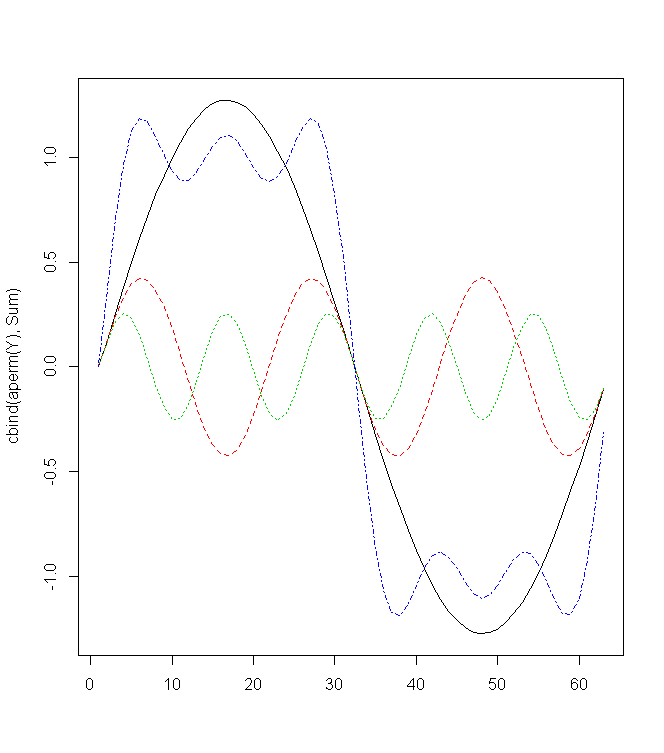
統計計算をするのにはどのソフトが一番便利でしょうか。簡単な計算であれば、EXCELなどの表計算ソフトが使いやすいかもしれません。 しかし、EXCELには、いくつかの問題点が存在している上に、それらがいつまでたっても修正されず、科学的に間違った結論を 出してしまう可能性が指摘されています。また、ある程度大きいデータだと、EXCELでは操作するのに時間がかかります。 （EXCELの間違いについて、詳しくは ひどい話です などを参照すればわかります。）
では、他のソフトはあるのかといえば、実はいろいろとあります。ここでとりあげるRというソフトは、フリー(GNU)でしかも かなり使い勝手の良いものです。

参考になるページ

Octaveとの書き方の比較

ここには、Octaveとのちょっとした文法の比較を記しています。Octaveは行列などの数値計算に強いと言われていますが、 RでもATLASなどを使用できるので、自分の使う範囲ではあまり 違いが感じられません。線型の計算で差がでるのでしょうか。

正弦波の加算（矩形波） 行列の使い方

たいした違いはありません。やはり、うまく短く書くためには、ある程度関数を知っている必要があるようです。実は、Octaveは Gnuplotなど外部のプログラムを呼び出してグラフなどを書いているので、その点には注意する必要があるかもしれません。

R

x = 0:62/10
A = c(1.2732, 0.4244, 0.2546)
h = c(1,3,5)
Sum = matrix(0, length(x), 1)
Y = matrix(0, nrow=length(A), ncol=length(x)) 
for (i in 1:3) {
Y[i,] <- A[i] * sin(h[i] * x)
Sum = Sum + Y[i,]
}
matplot(cbind(aperm(Y),Sum), pch=1:4, type="l")

Octave

x = 0:0.1:pi*2;
A = [1.2732 0.4244 0.2546];
h = [1 3 5];
Sum = zeros(1,63)
for i = 1:3
Y(i, :) = A(i) * sin(h(i) * x);
Sum = Sum + Y(i, :);
end
plot(x, Y, x, Sum);

Fourier変換

参考までに。また、；をつけるかで評価が変わってくるので、注意するとよいでしょう。

R

n = 512
nh = n/2
t = 0:n-1
Fs = 51.2
A = c(1.2732, 0.4244, 0.2546)
h = c(1, 3, 5) * 2 * pi
Sum = matrix(0, length(t), 1)
Y = matrix(0, nrow=length(A), ncol=length(t)) 
for (i in 1:3) {
        Y[i,] <- A[i] * sin(h[i] * t / Fs)
        Sum = Sum + Y[i,]
}

Y = fft(Sum)
Z = abs(Y)/(n/2)
f = t/n*Fs
plot(f[1:n/2], Z[1:n/2], type="l")

Octave

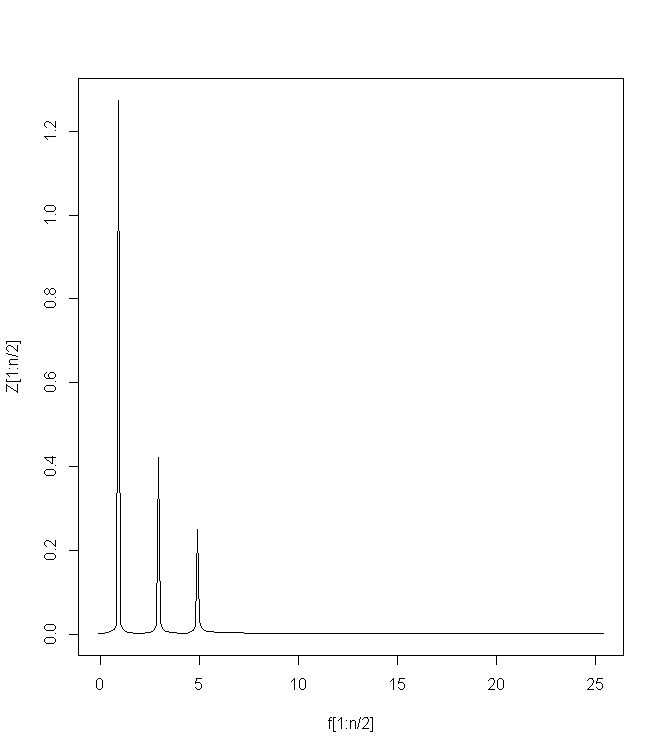
clear;
n = 512;
nh = n/2;
t = 0:n-1;
Fs = 51.2;
A = [1.2732 0.4244 0.2546];
h = [1 3 5] * 2 * pi;

Sum = zeros(1, n);
for i = 1:3
y(i, :) = A(i) * sin(h(i) * t / Fs);
Sum = Sum + y(i, :);
end

Y = fft(Sum, n);
Z = abs(Y)/256;
f = (0:n-1) / n * Fs;
plot(f(1:nh), Z(1:nh));

Tips

グローバル変数、永続付値

通常、=や<-といった代入は、関数などいわゆる｛｝で囲まれた部分のみで有効であり、Rでも同じである。だから、関数において 関数の外で使われている変数に書き込むには=や<-は使えない。 

> a <- 1
> b <- 2
> func <- function(){a <- 2;b <<- 3;print(a);print(b)}
> func()
[1] 2
[1] 3
> print(a)
[1] 1
> print(b)
[1] 3

この例では、グローバル変数a,bはそれぞれ1,2で初期化され、func()では、ローカル変数のa,グローバル変数のbにそれぞれ2,3 を代入したことになる。 

Rule of Open-Source Programming #34:

Every successful project will eventually spawn a sub-project

    -- Shlomi Fish
    -- "Rules of Open Source Programming"

I only discovered this myself quite recently. When Yahoo bought Viaweb, they
asked me what I wanted to do. I had never liked the business side very much,
and said that I just wanted to hack. When I got to Yahoo, I found that what
hacking meant to them was implementing software, not designing it. Programmers
were seen as technicians who translated the visions (if that is the word) of
product managers into code.

This seems to be the default plan in big companies. They do it because it
decreases the standard deviation of the outcome. Only a small percentage of
hackers can actually design software, and it's hard for the people running a
company to pick these out. So instead of entrusting the future of the software
to one brilliant hacker, most companies set things up so that it is designed
by committee, and the hackers merely implement the design.

If you want to make money at some point, remember this, because this is one of
the reasons startups win. Big companies want to decrease the standard
deviation of design outcomes because they want to avoid disasters. But when
you damp oscillations, you lose the high points as well as the low. This is
not a problem for big companies, because they don't win by making great
products. Big companies win by sucking less than other big companies.

    -- Paul Graham
    -- Hackers and Painters ( http://www.paulgraham.com/hp.html )

Powered by UNIX fortune(6)
[ Main Page ]