執筆時はR 3.4.1で行った。一部のパッケージ名は変更されているので、旧バージョンを使用する場合は、別名を使う必要があるかもしれない。
install.packages("Epi")
install.packages("pROC")
install.packages("epiDisplay") # 旧epicalc, logistic.display()
install.packages("ROCR")
install.packages("boot")
install.packages("car") # vif
install.packages("PredictABEL") # NDI reclassification
library(Epi)
library(pROC)
library(epiDisplay)
library(ROCR)
library(boot)
library(car)
library(PredictABEL)
ID,vestibular,age,AP.closed.rubber.MF.AUC,LR.closed.rubber.MF.AUC,AP.closed.rubber.Total.AUC,LR.closed.rubber.Total-AUC,closed.rubber.vel.,closed.rubber.area
1201,0 ,15,0.523426212,0.269885006,0.820424406,0.414206021,3.27746,9.10135
1202,0 ,15,0.351072044,0.223578706,0.736198925,0.371211784,2.96723,7.46619
1203,0 ,15,0.265367518,0.173022108,0.514121107,0.246539771,3.29103,6.13298
1204,0 ,15,0.353626616,0.238177879,0.463714611,0.366790223,1.91632,5.73948
1205,0 ,15,0.169586899,0.126551565,0.557775433,0.244873518,2.1595,4.99572
1206,0 ,15,0.269394935,0.206403073,0.393509107,0.334897681,2.59966,5.92069
1207,0 ,15,0.424102537,0.393463788,1.168681291,0.544718388,2.81974,12.77118
1208,0 ,16,0.412487956,0.326645509,0.535793678,0.47033513,2.43657,8.44789
1209,0 ,16,0.469543914,0.230436026,0.855767493,0.344026976,3.03804,9.62845
1210,0 ,16,0.782838708,0.45587768,1.521906139,0.681959862,4.68328,16.24997
2210,0 ,21,0.391552961,0.230276891,0.761130581,0.401299195,2.3379,8.19391
2212,0 ,22,0.505144485,0.40641785,0.7181703,0.614968708,1.96046,9.1636
...
115,1 ,27,2.293283199,1.860312519,2.703063836,2.383459171,5.387,41.24671
119,1 ,30,3.88273066,2.270253956,4.400436492,2.617610345,8.3377,65.19868
113,1 ,31,5.293441219,4.241308871,6.426775757,5.216305625,8.67859,123.03445
114,1 ,32,0.799501695,0.30278924,0.893147487,0.35387103,2.53165,7.8428
110,1 ,34,1.419653245,0.620747457,1.864303991,0.735879483,4.81428,22.87334
...
一般的なCSVファイルでデータを作成した。今回は、変数vestibularを他の変量から推定できるか評価するのが目的である。
一般的に10を越えるようだと要注意となっている。下記だと、いくつかの変数は注意が必要ということになる。
dp <- glm(z~x1+x2+x3+x4+x5+x6+x7, family="binomial", data=xdata)
print(vif(dp))
x1 x2 x3 x4 x5 x6 x7
1.311508 4.958128 17.973517 8.022008 20.809838 2.622894 16.597370
cls <- function(){ while(dev.cur() > 1) {dev.off()} }
cls()
vtTable <- read.csv("r3-data.csv", fileEncoding="cp932")
z <- vtTable$vestibular
x1 <- vtTable$age
x2 <- vtTable$AP.closed.rubber.MF.AUC
x3 <- vtTable$LR.closed.rubber.MF.AUC
x4 <- vtTable$AP.closed.rubber.Total.AUC
x5 <- vtTable$LR.closed.rubber.Total.AUC
x6 <- vtTable$closed.rubber.vel.
x7 <- vtTable$closed.rubber.area
xdata <- data.frame(x1=x1,x2=x2,x3=x3,x4=x4,x5=x5,x6=x6,x7=x7,z=z)
# normal ROC display
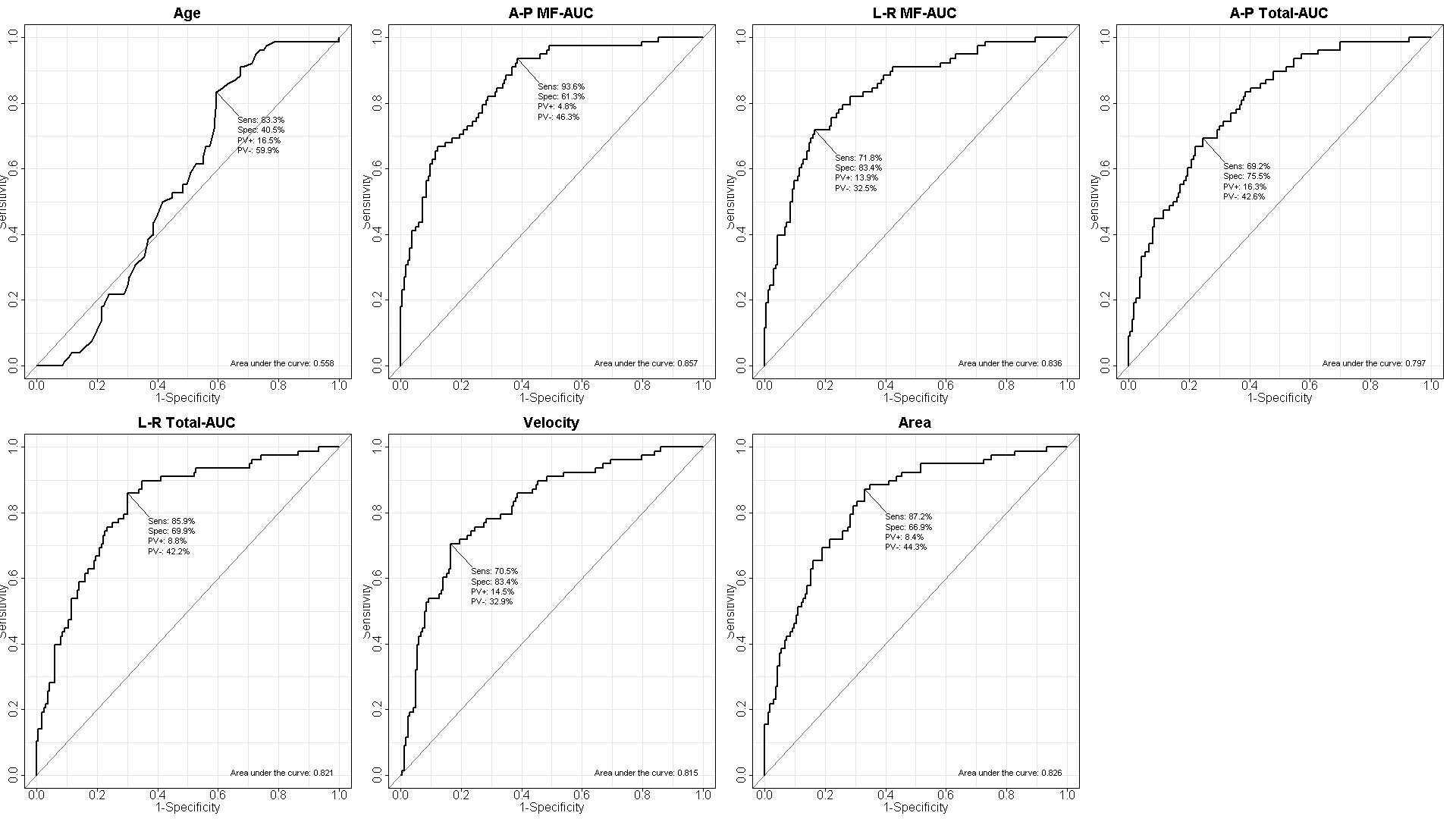
par(mfrow=c(2,4), ps=24)
Epi::ROC(form= z~x1, plot="ROC", PV=T, MX=F, MI=F, AUC=T, main="Age")
Epi::ROC(form= z~x2, plot="ROC", PV=T, MX=F, MI=F, AUC=T, main="A-P MF-AUC")
Epi::ROC(form= z~x3, plot="ROC", PV=T, MX=F, MI=F, AUC=T, main="L-R MF-AUC")
Epi::ROC(form= z~x4, plot="ROC", PV=T, MX=F, MI=F, AUC=T, main="A-P Total-AUC")
Epi::ROC(form= z~x5, plot="ROC", PV=T, MX=F, MI=F, AUC=T, main="L-R Total-AUC")
Epi::ROC(form= z~x6, plot="ROC", PV=T, MX=F, MI=F, AUC=T, main="Velocity")
Epi::ROC(form= z~x7, plot="ROC", PV=T, MX=F, MI=F, AUC=T, main="Area")
dev.copy(bmp, file="r3-normalROC.bmp", width=1920, height=1080, pointsize=10)
cls()

上記Epiパッケージ以外にも様々なパッケージがあるので、場合に応じて選べば良い。Epiパッケージ、pROCパッケージ、ROCRパッケージとglmの組み合わせの例を示した。また、下記ではz~x1の例を示した。 glmでロジスティック回帰を行ってからROCR::predictionを行うのは、中で行われる演算が理解できて良いかもしれない。
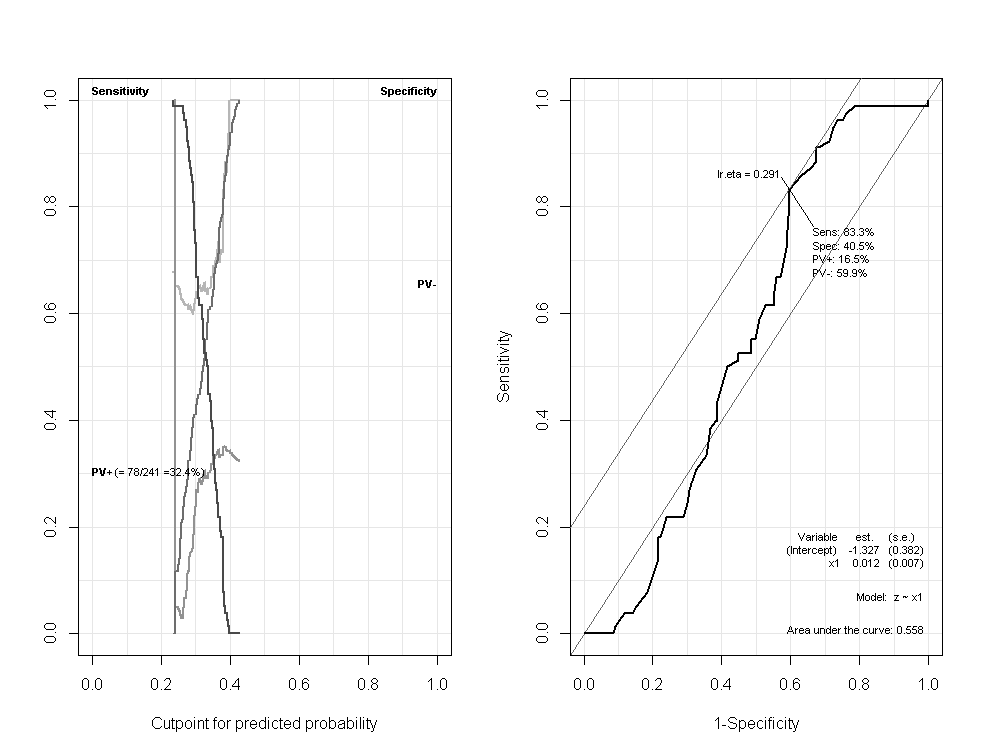
# Epiパッケージ
par(mfrow=c(1,2), ps=12)
a <- Epi::ROC(form= z~x1)
print(a$AUC)
# pROCパッケージのauc関数
pROC::auc(form=z~x1)
# ROCRパッケージの関数とglmによるロジスティック回帰を組み合わせる
afit <- glm(z~x1, data=xdata, family=binomial)
afit.predict <- ROCR::prediction(fitted(afit), xdata$z)
aperf <- ROCR::performance(afit.predict, "auc")
print(aperf) # print(aperf@y.values)でも良い
# こちらのパッケージでも、下記でROC曲線を書ける
aperf2 <- ROCR::performance(afit.predict, "tpr", "fpr")
par(mfrow=c(1,1), ps=12)
plot(aperf2)
# オッズ比はglmの結果から算出される
cat("OR\n")
exp(coef(afit))
[1] 0.5583215
Area under the curve: 0.5583
An object of class "performance"
Slot "x.name":
[1] "None"
Slot "y.name":
[1] "Area under the ROC curve"
Slot "alpha.name":
[1] "none"
Slot "x.values":
list()
Slot "y.values":
[[1]]
[1] 0.5583215
Slot "alpha.values":
list()
OR
(Intercept) x1
0.2652016 1.0116140
sink()で出力結果をファイルに保存できる。pROCにブートストラップ法が組み込まれているので、DeLong法以外にbootstrapも指定して信頼区間を計算できる。 マニュアルによると、percentile method (Carpenter and Bithell (2000) sections 2.1 and 3.3.) を使用しているとのことである。下記では2変数のみ表示しているが、他の変数も同様に表示可能。
d1 <- glm(z~x1, family="binomial")
d2 <- glm(z~x2, family="binomial")
d3 <- glm(z~x3, family="binomial")
d4 <- glm(z~x4, family="binomial")
d5 <- glm(z~x5, family="binomial")
d6 <- glm(z~x6, family="binomial")
d7 <- glm(z~x7, family="binomial")
r1 <- pROC::roc(form= z~x1)
r2 <- pROC::roc(form= z~x2)
r3 <- pROC::roc(form= z~x3)
r4 <- pROC::roc(form= z~x4)
r5 <- pROC::roc(form= z~x5)
r6 <- pROC::roc(form= z~x6)
r7 <- pROC::roc(form= z~x7)
sink(file="results.txt")
cat("x1 Age\n")
cat("x2 A-P MF-AUC\n")
cat("x3 L-R MF-AUC\n")
cat("x4 A-P Total-AUC\n")
cat("x5 L-R Total-AUC\n")
cat("x6 Velocity\n")
cat("x7 Area\n")
cat("--------------------------------------\n")
cat(" Age - Vestibular disorder\n")
cat("--------------------------------------\n")
print(summary(d1))
print(r1)
cat("CI of AUC\n")
print(pROC::ci.auc(r1, method = "delong",progress="none"))
set.seed(3141592)
print(pROC::ci.auc(r1, method = "boot", boot.n=2000, boot.stratified=TRUE,reuse.auc=TRUE,progress="none"))
cat("--------------------------------------\n")
cat(" A-P MF-AUC - Vestibular disorder\n")
cat("--------------------------------------\n")
print(summary(d2))
print(r2)
print(pROC::ci.auc(r2, method = "delong",progress="none"))
set.seed(3141592)
print(pROC::ci.auc(r2, method = "boot", boot.n=2000, boot.stratified=TRUE,reuse.auc=TRUE))
sink()
x1 Age
x2 A-P MF-AUC
x3 L-R MF-AUC
x4 A-P Total-AUC
x5 L-R Total-AUC
x6 Velocity
x7 Area
--------------------------------------
Age - Vestibular disorder
--------------------------------------
Call:
glm(formula = z ~ x1, family = "binomial")
Deviance Residuals:
Min 1Q Median 3Q Max
-1.0531 -0.9267 -0.7941 1.4197 1.7056
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.327265 0.381908 -3.475 0.00051 ***
x1 0.011547 0.006847 1.686 0.09172 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 303.46 on 240 degrees of freedom
Residual deviance: 300.57 on 239 degrees of freedom
AIC: 304.57
Number of Fisher Scoring iterations: 4
Call:
roc.formula(formula = z ~ x1)
Data: x1 in 163 controls (z 0) < 78 cases (z 1).
Area under the curve: 0.5583
CI of AUC
95% CI: 0.487-0.6296 (DeLong)
95% CI: 0.4879-0.6288 (2000 stratified bootstrap replicates)
--------------------------------------
A-P MF-AUC - Vestibular disorder
--------------------------------------
Call:
glm(formula = z ~ x2, family = "binomial")
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1785 -0.6104 -0.4418 0.4760 2.2663
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.4674 0.4266 -8.129 4.33e-16 ***
x2 2.9945 0.4360 6.868 6.51e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 303.46 on 240 degrees of freedom
Residual deviance: 212.67 on 239 degrees of freedom
AIC: 216.67
Number of Fisher Scoring iterations: 5
Call:
roc.formula(formula = z ~ x2)
Data: x2 in 163 controls (z 0) < 78 cases (z 1).
Area under the curve: 0.8567
95% CI: 0.8078-0.9056 (DeLong)
95% CI: 0.8058-0.901 (2000 stratified bootstrap replicates)
sink()はappendで追記可能である。全変数によるモデルのAUCを算出するため、ブートストラップ用にauc_calcを定義しbootで信頼区間を算出した。 glm(family=binomial)でロジスティック回帰を行い、ROCRパッケージのprediction及びperformanceを用いて算出した。 例として挙げており、多重共線性は無視し、すべての変数を入れたモデルでの算出を行っている。
sink(file="results.txt", append=TRUE)
cat("Calculating bootstrap multivariate logistic AUC CI ...\n")
auc_calc <- function(data, indices, formula) {
d <- data[indices,]
afit <- glm(formula, data=d, family=binomial)
afit.predict <- ROCR::prediction(fitted(afit), d$z)
aperf <- ROCR::performance(afit.predict, "auc")
return(aperf@y.values[[1]])
}
set.seed(3141592)
boot.results <- boot(data=xdata, statistic=auc_calc, R=2000, formula=z~x1+x2+x3+x4+x5+x6+x7)
print(boot.ci(boot.results,type = c("norm","basic","perc","bca")))
sink()
Calculating bootstrap multivariate logistic AUC CI ...
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates
CALL :
boot.ci(boot.out = boot.results, type = c("norm", "basic", "perc",
"bca"))
Intervals :
Level Normal Basic
95% ( 0.8116, 0.9017 ) ( 0.8149, 0.9028 )
Level Percentile BCa
95% ( 0.8441, 0.9320 ) ( 0.8072, 0.9016 )
Calculations and Intervals on Original Scale
Warning : BCa Intervals used Extreme Quantiles
Some BCa intervals may be unstable
警告メッセージ:
In norm.inter(t, adj.alpha) : extreme order statistics used as endpoints
pROCのrocでも同様にオプションを指定してブートストラップ法を用いて信頼区間を求められる。結果はpercentile methodのみである。
afit <- glm(z~x1+x2+x3+x4+x5+x6+x7,data=xdata,binomial)
rr1 <- pROC::roc(predictor=fitted(afit), response=xdata$z)
set.seed(3141592)
pROC::ci.auc(rr1, method="boot", boot.n=2000, boot.stratified=TRUE, reuse.auc=FALSE)
95% CI: 0.8279-0.9173 (2000 stratified bootstrap replicates)
オッズ比はglmで算出可能である。ブートストラップ法で信頼区間を求める場合、expにかける前にブートストラップを行うので、boot.ciでh=expにより戻す必要がある。 例として示しているだけで、信頼区間自体はかなり広めの値が算出されている。
# ORの表示
afit <- glm(z~x1+x2+x3+x4+x5+x6+x7,data=xdata,binomial)
print(exp(coef(afit)))
# ORの表示(こちらの方が一般的)
epiDisplay::logistic.display(afit, crude.p.value=TRUE, decimal=5)
# boot用の関数
m_oddsratio_calc <- function(data, indices, formula) {
d <- data[indices,]
afit <- glm(formula, data=d, family=binomial)
return(coef(afit))
}
boot.results <- boot(data=data, statistic=m_oddsratio_calc, R=2000, formula=z~x1+x2+x3+x4+x5+x6+x7)
or_results <- c()
# n=vn variates
for(it in 1:length(boot.results$t0))
{
btor <- boot.ci(boot.results, type = c("perc","bca"), index=it, h=exp)
or_results <- rbind(or_results, c(btor$percent[4:5], btor$bca[4:5]))
}
or_result <- data.frame(t(or_results))
colnames(or_results) <- c("(percentile L,", "percentile H)", "(BCa L,", "BCa H)")
rownames(or_results) <- names(boot.results$t0)
options(width=120)
options(scipen=5)
options(digits=5)
print(or_results)
options(digits=5)
(Intercept) x1 x2 x3 x4 x5 x6 x7
0.06057367 0.99038448 67.91379358 92.14700498 0.13143789 0.05736990 0.98885931 1.05722083
Logistic regression predicting z
crude OR(95%CI) crude P value adj. OR(95%CI) P(Wald's test) P(LR-test)
x1 (cont. var.) 1.01161 (0.99813,1.02528) 0.09172 0.9904 (0.9708,1.0103) 0.341842 0.339253
x2 (cont. var.) 19.97557 (8.49905,46.94919) < 0.001 67.91379 (8.9655,514.44803) < 0.001 < 0.001
x3 (cont. var.) 16.0072 (6.93308,36.95767) < 0.001 92.147 (2.73443,3105.24416) 0.01172 0.008423
x4 (cont. var.) 4.52786 (2.74095,7.4797) < 0.001 0.13144 (0.02714,0.63655) 0.011697 0.005698
x5 (cont. var.) 6.34097 (3.45989,11.62112) < 0.001 0.05737 (0.00381,0.8649) 0.03894 0.039388
x6 (cont. var.) 1.743 (1.44319,2.10511) < 0.001 0.98886 (0.73993,1.32154) 0.939644 0.939816
x7 (cont. var.) 1.12331 (1.08236,1.16581) < 0.001 1.05722 (0.90692,1.23244) 0.476972 0.478855
Log-likelihood = -98.2572877
No. of observations = 241
AIC value = 212.5145753
(percentile L, percentile H) (BCa L, BCa H)
(Intercept) 0.00991018 0.13853 0.0222085 0.23269
x1 0.96480127 1.00792 0.9719215 1.01271
x2 12.82765327 110116.95166 4.9532801 3076.21182
x3 1.14584657 9811.50194 1.2475637 12605.13843
x4 0.00042035 0.60076 0.0028145 2.35539
x5 0.00178572 3.18766 0.0014440 2.33899
x6 0.71145651 2.06223 0.5876320 1.60159
x7 0.84439828 1.33158 0.8639421 1.34545
ステップワイズ法により、vestibularを推定するのに適切な変数を探索し(モデルを選択)、x2x3x4x5が選択された。例として示しているので、実際には多重共線性に注意が必要となる。 繰り返しになるが、それぞれでオッズ比を表示させている。Crude ORは交絡補正前で、いわゆる単変量と同じだが、adj. (adjusted) ORは多変量であり、値が異なることが確認できる。
sink(file="results.txt", append=TRUE)
cat("======================================\n")
cat(" Multivariate analysis\n")
cat("======================================\n")
cat("x1 Age\n")
cat("x2 A-P MF-AUC\n")
cat("x3 L-R MF-AUC\n")
cat("x4 A-P Total-AUC\n")
cat("x5 L-R Total-AUC\n")
cat("x6 Velocity\n")
cat("x7 Area\n")
# stepwise logistic analysis
dp <- glm(z~x1+x2+x3+x4+x5+x6+x7, family="binomial", data=xdata)
d_null<- glm(z~1,family=binomial)
# linear
print(summary(dp))
cat("----------------------------------------------------------\n")
cat("(crude OR (odds ratio): bivariate / adj. OR: multivariate)\n")
print(logistic.display(dp,crude.p.value=TRUE,decimal=5))
cat("----------------------------------------------------------\n")
cat("\n\nStepwise logistic analysis -->>\n")
d_step <- step(d_null,scope=formula(dp),direction="both")
print(summary(d_step))
cat("----------------------------------------------------------\n")
cat("(crude OR (odds ratio): bivariate / adj. OR: multivariate)\n")
print(logistic.display(d_step,crude.p.value=TRUE,decimal=5))
#print(fitted(d_step)[2])
cat("----------------------------------------------------------\n")
pred <- ROCR::prediction(fitted(d_step), z)
perf <- performance(pred,"tpr","fpr")
perf1 <- performance(pred,"auc")
M <- max(perf@y.values[[1]]-perf@x.values[[1]])
d_cutoff <- which(perf@y.values[[1]]-perf@x.values[[1]]==M)
cat("Cutoff: ")
print(perf@alpha.values[[1]][d_cutoff])
cat("Sensitivity: ")
print(perf@y.values[[1]][d_cutoff])
cat("Specificity: ")
print(1-perf@x.values[[1]][d_cutoff])
cat("AUC: ")
print(perf1@y.values)
sink()
======================================
Multivariate analysis
======================================
x1 Age
x2 A-P MF-AUC
x3 L-R MF-AUC
x4 A-P Total-AUC
x5 L-R Total-AUC
x6 Velocity
x7 Area
Call:
glm(formula = z ~ x1 + x2 + x3 + x4 + x5 + x6 + x7, family = "binomial",
data = xdata)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.5208 -0.6000 -0.4015 0.3201 2.5119
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.803895 0.578336 -4.848 1.25e-06 ***
x1 -0.009662 0.010165 -0.951 0.3418
x2 4.218239 1.033108 4.083 4.44e-05 ***
x3 4.523385 1.794657 2.520 0.0117 *
x4 -2.029221 0.804880 -2.521 0.0117 *
x5 -2.858235 1.384256 -2.065 0.0389 *
x6 -0.011203 0.147961 -0.076 0.9396
x7 0.055644 0.078241 0.711 0.4770
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 303.46 on 240 degrees of freedom
Residual deviance: 196.51 on 233 degrees of freedom
AIC: 212.51
Number of Fisher Scoring iterations: 6
----------------------------------------------------------
(crude OR (odds ratio): bivariate / adj. OR: multivariate)
Logistic regression predicting z
crude OR(95%CI) crude P value
x1 (cont. var.) 1.01161 (0.99813,1.02528) 0.09172
x2 (cont. var.) 19.97557 (8.49905,46.94919) < 0.001
x3 (cont. var.) 16.0072 (6.93308,36.95767) < 0.001
x4 (cont. var.) 4.52786 (2.74095,7.4797) < 0.001
x5 (cont. var.) 6.34097 (3.45989,11.62112) < 0.001
x6 (cont. var.) 1.743 (1.44319,2.10511) < 0.001
x7 (cont. var.) 1.12331 (1.08236,1.16581) < 0.001
adj. OR(95%CI) P(Wald's test) P(LR-test)
x1 (cont. var.) 0.9904 (0.9708,1.0103) 0.341842 0.339253
x2 (cont. var.) 67.91379 (8.9655,514.44803) < 0.001 < 0.001
x3 (cont. var.) 92.147 (2.73443,3105.24416) 0.01172 0.008423
x4 (cont. var.) 0.13144 (0.02714,0.63655) 0.011697 0.005698
x5 (cont. var.) 0.05737 (0.00381,0.8649) 0.03894 0.039388
x6 (cont. var.) 0.98886 (0.73993,1.32154) 0.939644 0.939816
x7 (cont. var.) 1.05722 (0.90692,1.23244) 0.476972 0.478855
Log-likelihood = -98.2572877
No. of observations = 241
AIC value = 212.5145753
----------------------------------------------------------
Stepwise logistic analysis -->>
Start: AIC=305.46
z ~ 1
Df Deviance AIC
+ x2 1 212.67 216.67
+ x3 1 226.45 230.45
+ x7 1 233.71 237.71
+ x5 1 240.02 244.02
+ x4 1 246.26 250.26
+ x6 1 254.95 258.95
+ x1 1 300.57 304.57
<none> 303.46 305.46
Step: AIC=216.67
z ~ x2
Df Deviance AIC
+ x4 1 206.84 212.84
+ x1 1 209.94 215.94
<none> 212.67 216.67
+ x7 1 211.89 217.89
+ x3 1 211.91 217.91
+ x6 1 212.60 218.60
+ x5 1 212.65 218.65
- x2 1 303.46 305.46
Step: AIC=212.85
z ~ x2 + x4
Df Deviance AIC
+ x3 1 203.36 211.36
+ x1 1 204.50 212.50
<none> 206.84 212.84
+ x7 1 206.26 214.26
+ x6 1 206.45 214.45
+ x5 1 206.49 214.49
- x4 1 212.67 216.67
- x2 1 246.26 250.26
Step: AIC=211.36
z ~ x2 + x4 + x3
Df Deviance AIC
+ x5 1 198.01 208.01
+ x1 1 201.28 211.28
<none> 203.36 211.36
- x3 1 206.84 212.84
+ x7 1 202.87 212.87
+ x6 1 203.35 213.35
- x4 1 211.91 217.91
- x2 1 226.44 232.44
Step: AIC=208.01
z ~ x2 + x4 + x3 + x5
Df Deviance AIC
<none> 198.01 208.01
+ x1 1 197.06 209.06
+ x7 1 197.49 209.49
+ x6 1 198.01 210.01
- x5 1 203.36 211.36
- x3 1 206.49 214.49
- x4 1 207.28 215.28
- x2 1 220.60 228.60
Call:
glm(formula = z ~ x2 + x4 + x3 + x5, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.5236 -0.5916 -0.4127 0.3756 2.4989
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.1744 0.4475 -7.094 1.30e-12 ***
x2 4.1636 0.9819 4.240 2.23e-05 ***
x4 -1.7143 0.6202 -2.764 0.00570 **
x3 4.6937 1.6972 2.766 0.00568 **
x5 -2.5296 1.1269 -2.245 0.02478 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 303.46 on 240 degrees of freedom
Residual deviance: 198.01 on 236 degrees of freedom
AIC: 208.01
Number of Fisher Scoring iterations: 6
----------------------------------------------------------
(crude OR (odds ratio): bivariate / adj. OR: multivariate)
Logistic regression predicting z
crude OR(95%CI) crude P value
x2 (cont. var.) 19.97557 (8.49905,46.94919) < 0.001
x4 (cont. var.) 4.52786 (2.74095,7.4797) < 0.001
x3 (cont. var.) 16.0072 (6.93308,36.95767) < 0.001
x5 (cont. var.) 6.34097 (3.45989,11.62112) < 0.001
adj. OR(95%CI) P(Wald's test) P(LR-test)
x2 (cont. var.) 64.30488 (9.38546,440.58741) < 0.001 < 0.001
x4 (cont. var.) 0.18009 (0.05341,0.60724) 0.005704 0.002323
x3 (cont. var.) 109.26169 (3.92485,3041.67751) 0.005682 0.00358
x5 (cont. var.) 0.07969 (0.00875,0.72547) 0.024783 0.020735
Log-likelihood = -99.0044212
No. of observations = 241
AIC value = 208.0088424
----------------------------------------------------------
Cutoff: [1] 0.342448
Sensitivity: [1] 0.7692308
Specificity: [1] 0.8220859
AUC: [[1]]
[1] 0.8695926
pROCにあるroc.testを使うと、モデル間でAUCを比較し、どちらのモデルが優位か算出することが出来る。
compare_auc <- function(formula1, formula2, data, response, alternative="two.sided"){
olm1 <- glm(formula1, data=data, family="binomial")
olm2 <- glm(formula2, data=data, family="binomial")
ROC_1 <- pROC::roc(response=response, predictor=fitted(olm1))
ROC_2 <- pROC::roc(response=response, predictor=fitted(olm2))
print(pROC::roc.test(ROC_1, ROC_2, method="delong", alternative=alternative))
print(pROC::roc.test(ROC_1, ROC_2, method = "bootstrap", boot.n = 2000, progress="none", alternative=alternative))
}
compare_auc(z~x1+x3,z~x1+x2+x3+x4+x5+x6+x7,xdata,xdata$z,"less")
DeLong's test for two correlated ROC curves
data: ROC_1 and ROC_2
Z = -2.2, p-value = 0.014
alternative hypothesis: true difference in AUC is less than 0
sample estimates:
AUC of roc1 AUC of roc2
0.83113 0.87345
Bootstrap test for two correlated ROC curves
data: ROC_1 and ROC_2
D = -2.25, boot.n = 2000, boot.stratified = 1, p-value = 0.012
alternative hypothesis: true difference in AUC is less than 0
sample estimates:
AUC of roc1 AUC of roc2
0.83113 0.87345
PredictABELのreclassificationを用いて、NRI(net reclassification improvement)とIDI(integrated discrimination improvement)を算出することが出来る。
ndi_calc <- function(formula1, formula2, data, resp){
olm1 <- glm(formula1, data=data, family="binomial")
olm2 <- glm(formula2, data=data, family="binomial")
PredictABEL::reclassification(data=data,cOutcome=resp,predrisk1=fitted(olm1),predrisk2=fitted(olm2),cutoff=c(0,0.5,1))
}
ndi_calc(z~x1+x3,z~x1+x2+x3+x4+x5+x6+x7,xdata,8) # outcomeが8列目(=z)にあるのを指定
_________________________________________
Reclassification table
_________________________________________
Outcome: absent
Updated Model
Initial Model [0,0.5) [0.5,1] % reclassified
[0,0.5) 145 3 2
[0.5,1] 4 11 27
Outcome: present
Updated Model
Initial Model [0,0.5) [0.5,1] % reclassified
[0,0.5) 30 10 25
[0.5,1] 5 33 13
Combined Data
Updated Model
Initial Model [0,0.5) [0.5,1] % reclassified
[0,0.5) 175 13 7
[0.5,1] 9 44 17
_________________________________________
NRI(Categorical) [95% CI]: 0.0702 [ -0.0312 - 0.1716 ] ; p-value: 0.17454
NRI(Continuous) [95% CI]: 0.809 [ 0.5625 - 1.0556 ] ; p-value: 0
IDI [95% CI]: 0.0971 [ 0.054 - 0.1401 ] ; p-value: 0.00001
Excellent day for putting Slinkies on an escalator.
<integral> hi perly!
<perlygatekeeper> hey Chris, hey integral
<perlygatekeeper> dabreegster, don't know you do I but HEY anyway
<perlygatekeeper> what's been up?
<dabreegster> Ignore me, fine.
* dabreegster goes in a corner
<Chris62vw> dabreegster is the man, man
<dabreegster> Ah, that's better.
<rindolf> perlygatekeeper: yo, yo, yo, dude!
<perlygatekeeper> rindolf!!
<rindolf> perlygatekeeper: what's up?
<perlygatekeeper> hmmm
<perlygatekeeper> not much
<perlygatekeeper> you?
<rindolf> perlygatekeeper: fine. Let me recall what I said to
ezra.
<rindolf> perlygatekeeper: I'm fine. Got into a few flamewars,
and escaped alive to tell the tale.
<rindolf> perlygatekeeper: worked a bit on my story "The Human
Hacking Field Guide".
<rindolf> perlygatekeeper: (which, BTW, you appear there (as
your IRC nick at least)
<rindolf> perlygatekeeper: and now working on the Computer
Graphics section of my homepage.
<perlygatekeeper> rindolf, what the hell?
<rindolf> perlygatekeeper: excuse me?
<perlygatekeeper> rindolf was that someone pretending to be me?
<perlygatekeeper> I never said those things
<rindolf> perlygatekeeper: it's a fictitious story.
<rindolf> perlygatekeeper: relax.
<dabreegster> perlygatekeeper: or you could be the imposter right
now... or maybe just schizophrenic.
<rindolf> dabreegster: MPDed not schizophrenic.
<rindolf> dabreegster: schizophrenia is not
Multi-Persona-Disordered.
<b0at> perlygatekeeper: It's fan fiction from your fan!
<dabreegster> rindolf: what's the difference?
<rindolf> dabreegster: MPD is when there are several
personalities living inside your brain.
<rindolf> dabreegster: in schizophrenia, you have one I-ness,
but hear voices, hallucinate and stuff.
<dabreegster> rindolf: Ah. Why is it considered a disorder? MPD
could be quite useful... One would have different
perspectives on a subject.
<perlygatekeeper> where's beth, she'll know it's me
<integral> But how will we know it's beth?!
<dabreegster> rindolf: Oh, I have MPD then, not schizophrenia. I
don't hallucinate.
<dabreegster> integral: WE DON'T!
<b0at> I don't hallucinate, but my other personality does.
<dabreegster> How do I know all of you exist? Am I just a figment of
my own imagination?
<dabreegster> b0at: Interesting...
<rindolf> dabreegster: Julian Jaynes describes schizophrenia
very well in his "The Origins of Consciousness during
the Breakdown of the Bicameral Mind book".
<integral> nono, you're all just figments of _lilo_'s imagination
<dabreegster> rindolf: I'll check it out
<b0at> he wishes
<dabreegster> integral: and you?
<perlygatekeeper> the voices tell me if it's really beth or not
<dabreegster> perlygatekeeper: The voices tell me everything.
<dabreegster> Wait, I do have the Voices. Maybe I have MPD _and_
schizophrenia.
<b0at> Ah, but the question is: do the Voices have voices?
<rindolf> dabreegster:
http://en.wikipedia.org/wiki/The_Origin_of_Consciousness_in_the_Breakdown_of_the_Bicameral_Mind
<b0at> And if so, is it your own voice?
<dabreegster> b0at: And do the voices of the voices have voices?
<b0at> That's just going too far.
<dkr> don't worry, those are angels, invest in tarot cards
and you will be able to understand them
<dabreegster> b0at: and if it's not, then could it be the voice
of........ integral? rindolf? or.... buu!
<b0at> buu has other plans for our empty skulls
<dabreegster> b0at: and if they do, then what do the voices of the
voices of the voices of the Voices sound like?
<integral> *sob* it's the cabbages. The cabbages keep telling me
to do things
<Botje> really? most of the time it's the socks that tell me
stuff
<dabreegster> integral: The lawn gnomes tell me.
They're........everywhere...*sniffle*
<integral> *blubber* the socks are worse, there's moths living in
them
<dabreegster> The lawn gnomes tell me to stay away from Life. They
force me to write poetry.
<dabreegster> integral: *whispering* are the _moths_ the Voices? or
the voices of the Voices? or the voices of the voices
of the Voices?
* dabreegster goes back to reading
<integral> *looks furtively around for moths*
-- The voices told me so.
-- #perl, Freenode