Freeverb3§Œ≥´»Ø§Œ∫ð§À°¢ªƒ∂¡±Èªª§Œ§ø§·§Œ•«•£•Ï•§•È•§•Û≥»ª∂§Œ§ø§·§Œπ‘ŒÛ§»§∑§∆ª»§Ô§Ï§∆§§§Î
Hadamard matrix (•¢•¿•Þ°º•Îπ‘ŒÛ)
§Ú≥ÿΩ¨§π§Î§ø§·§ÀScilab§»Octave§Úª»§√§ø∫𧌵≠œø°£ºπ…ƪ˛§œScilab-6.0.0 / Octave-4.2.1§«π‘§√§ø§¨°¢Scilab§œ5∑œ§´§È6∑œ§À§ §√§∆§´§ §Í —§Ô§√§∆§§§Î§Œ§«°¢
∞Ï…Ù§Œ•Þ•Ø•Ì≈˘§«§œ∏þ¥π¿≠§¨§ §Ø§ §√§∆§§§Î°£5∑œ§Œ√ʧ«§‚°¢¬–±˛§π§ÎToolbox§¨∞€§ §Í°¢∏þ¥π¿≠§œ§´§ §ÍÀ≥§∑§§§»§≥§Ì§¨§¢§Î°£∏§ŒπýÃЧ«§œ°¢¡∞§ŒπýÃЧŒ¥ÿøÙ§À∞Õ¬∏§∑§∆§§§Î…Ù ¨§‚§¢§Î§Œ§«°¢∫«Ωȧ´§ÈΩÁ§Àº¬π‘§π§Î°£
√º≈™§À∏¿§®§–°¢Matlab§»∆±§∏§Ë§¶§ÀScilab§Úª»§™§¶§»§π§Î§»°¢§´§ §Í§Œ¥ÿøÙ§Ú≥∞…ÙToolbox§«•§•Û•π•»°º•Î§π§Î…¨Õ◊§¨Ω–§∆§Ø§Î§ø§·°¢•≥•¢§Œ§þ§Œ•§•Û•π•»°º•Î§Œ§þ§«Matlab§ŒSignal Processing Toolbox§‰
Image Processing Toolbox§»∆±≈˘§Àª»§§§ø§§øÕ§À§»§√§∆§œOctave§¨§™¥´§·§«§¢§Î°£Scilab§ŒÕ•∞ÿ≠§œ°¢Xcos≈˘§ŒGUI•◊•Ì•∞•È•þ•Û•∞§¨§«§≠§ÎΩͧ»§§§¶§≥§»§À§ §Î°£
±—∏Ï»«Windows§«∆¸ÀÐ∏Ï•Ì•±°º•Î§Œæı¬÷§«µØ∆∞§π§Î§» ∏ª˙≤Ω§±§π§Î§≥§»§¨§¢§Í°¢§Ω§ŒæÏπÁ§œ°¢≤ºµ≠§Œ§Ë§¶§À±—∏ϧڪÿƒÍ§π§Î§»Œ…§§°£
setdefaultlanguage('en_US')
Octave§«§œ…∏Ωý§«hadamard()¥ÿøÙ§¨ª»§®§Î§¨°¢Scilab§«§œ…∏Ωý§«§œª»§®§ §§§Ë§¶§«§¢§Î°£π‘ŒÛ¿∏¿Æ•Þ•Ø•Ì§¨≥´»Ø§µ§Ï§∆§§§Î¬æ°¢ Scilab 5∑œ§À§œImage_Processing_Toolbox_2(IPT2)§¨§¢§Í°¢hadamard()§‰fwht()§¨ª»§®§Î°£§≥§≥§À§œ¿ËΩ“§Œ•Þ•Ø•Ì§»√ª§Ø§∑§ø¥ÿøÙ§Ú∫Чª§Î°£ √¢§∑°¢§≥§ŒToolbox§Œfwht()§œMatlab§Œfwht()§»∆±§∏§Ø°¢∆Ûº°∏µ§Œπ‘ŒÛ§Ú∆˛Œœ§∑§∆§‚ŒÛÀ˧À±Èªª§π§Î§¿§±§«°¢∆Ûº°∏µ§ŒΩËÕ˝§Ú§∑§∆§Ø§Ï§Î§Ô§±§«§œ§ §§§Œ§«°¢ΩËÕ˝§œ§«§≠§∫°¢∏ÂΩ“§Œ ˝À°§«¬–±˛§π§Î°£
// makematrix_hadamard.sci
// Copyright (C) 2008-2009 - INRIA - Michael Baudin
//
// This file must be used under the terms of the CeCILL.
// This source file is licensed as described in the file COPYING, which
// you should have received as part of this distribution. The terms
// are also available at
// http://www.cecill.info/licences/Licence_CeCILL_V2-en.txt
//
// makematrix_hadamard --
// Returns the Hadamard matrix of size n.
// n is expected to be a power of 2.
// Arguments, input
// n : the size of the matrix to return
// Reference
// http://en.wikipedia.org/wiki/Hadamard_matrix
//
function a = makematrix_hadamard ( n )
pow2n = log2(n);
if ( n - 2^pow2n <>0 ) then
errmsg = msprintf(gettext("%s: n is expected to be a power of 2."), "makematrix_hadamard");
error(errmsg)
end
if n==1 then
a = ones(1,1)
else
m = int(n/2)
b = makematrix_hadamard(m)
a = zeros(n,n)
a(1:m,1:m) = b(1:m,1:m)
a(1:m,m+1:n) = b(1:m,1:m)
a(m+1:n,1:m) = b(1:m,1:m)
a(m+1:n,m+1:n) = -b(1:m,1:m)
end
endfunction
// hadamard.sci
// Copyright (C) 2008-2009 - INRIA - Michael Baudin
//
// This file must be used under the terms of the CeCILL.
// This source file is licensed as described in the file COPYING, which
// you should have received as part of this distribution. The terms
// are also available at
// http://www.cecill.info/licences/Licence_CeCILL_V2-en.txt
//
// hadamard --
// Returns the Hadamard matrix of size n.
// n is expected to be a power of 2.
// Arguments, input
// n : the size of the matrix to return
// Reference
// http://en.wikipedia.org/wiki/Hadamard_matrix
//
function a = hadamard ( n )
a = makematrix_hadamard ( n );
endfunction
--> hadamard(4) ans = 1. 1. 1. 1. 1. -1. 1. -1. 1. 1. -1. -1. 1. -1. -1. 1.
•®•È°º•¡•ß•√•Ø≈˘§œ§ §∑§«§‚§√§»¥ √±§ ƒÍµ¡§‚§«§≠§Î°£
function hmatrix=hadamard(n) h=[1,1;1,-1] hmatrix=h; for n = 1:1:(log2(n)+1)-2 // kron() - Kronecker product (.*.) hmatrix = hmatrix.*.h; end endfunction
•Ø•Ì•Õ•√•´°º¿— kron()§œ°¢Scilab°¢Octave§ŒŒæ ˝§«ª»§®§Î§¨°¢Scilab§«§œ°¢.*.§»§§§¶±Èªªª“§¨ª»§®§Î°£
GNU Octave, version 4.2.1 Copyright (C) 2017 John W. Eaton and others. This is free software; see the source code for copying conditions. There is ABSOLUTELY NO WARRANTY; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. For details, type 'warranty'. Octave was configured for "x86_64-w64-mingw32". Additional information about Octave is available at http://www.octave.org. Please contribute if you find this software useful. For more information, visit http://www.octave.org/get-involved.html Read http://www.octave.org/bugs.html to learn how to submit bug reports. For information about changes from previous versions, type 'news'. >> hadamard(8) ans = 1 1 1 1 1 1 1 1 1 -1 1 -1 1 -1 1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1 -1 -1 1 1 1 1 1 -1 -1 -1 -1 1 -1 1 -1 -1 1 -1 1 1 1 -1 -1 -1 -1 1 1 1 -1 -1 1 -1 1 1 -1 >>
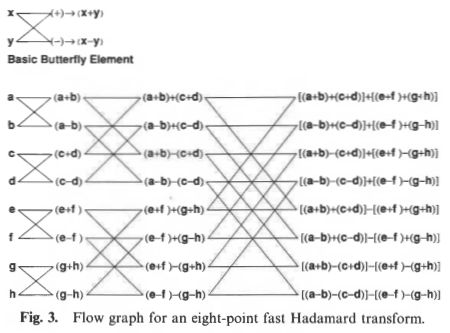
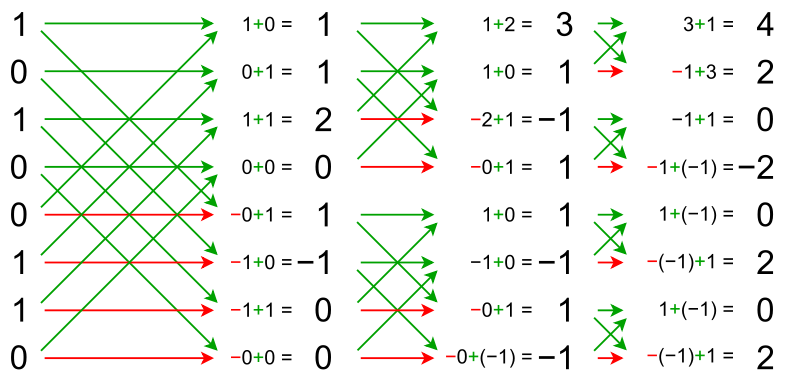
•¢•¿•Þ°º•Îπ‘ŒÛ§Œ¿≠º¡§´§È°¢•”•√•»±Èªª§»æÍÕæ±Èªª§«¿∏¿Æ§π§Î§≥§»§‚§«§≠§Î°£
dec2bin(0:7)-'0' (dec2bin(0:7)-'0')' mod((dec2bin(0:7)-'0') * (dec2bin(0:7)-'0')', 2) mod((dec2bin(0:7)-'0') * (dec2bin(0:7)-'0')', 2) * (-2) + 1
ans = 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 ans = 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 ans = 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 1 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 1 0 1 0 0 1 ans = 1 1 1 1 1 1 1 1 1 -1 1 -1 1 -1 1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1 -1 -1 1 1 1 1 1 -1 -1 -1 -1 1 -1 1 -1 -1 1 -1 1 1 1 -1 -1 -1 -1 1 1 1 -1 -1 1 -1 1 1 -1
æµ≠§«¿∏¿Æ§µ§Ï§øπ‘ŒÛ§ÚHadamard ordered (Natural ordered§Þ§ø§œSylvester) Matrix§»∏∆§÷§¨°¢øÆπÊΩËÕ˝§‰≤Ë¡¸ΩËÕ˝≈˘§«π‘§¶§Ë§¶§ ƒ„º˛«»§´§Èπ‚º˛«»§ÀΩÁ§À —¥π§µ§Ï§øπ‘ŒÛ§‚§¢§Í°¢ §≥§Ï§œSequency ordered Walsh-Hadamard Matrix§»∏∆§÷°£§≥§Œ∑∏øÙΩÁΩ¯§œ°¢ •∞•Ï•§•≥°º•…§Œ•”•√•»»ø≈槌ΩÁ§À§ §√§∆§§§Î°£§Ω§Œ¬æ§À∑∏øÙΩÁΩ¯§¨•∞•Ï•§•≥°º•…ΩÁ§ŒDyadic ordered (Paley ordered) Matrix§»§§§¶§Œ§‚§¢§Î°£ ∫«∂·§¿§»FPGAº¬¡ı§Œœ¿ ∏§À¥ ∑ȧ ¿‚ÿ§¨∫Ч√§∆§§§Î°£ ƒÃæÔ§Œ•–•ø•’•È•§±Èªª§À§Ë§ÎFast Walsh-Hadamard Transform (π‚¬Æ•¢•¿•Þ°º•Î —¥π)§Ú𑧶§ø§·§À§œ°¢ Hadamard ordered Matrix§«§ §±§Ï§–§ §È§∫°¢§Ω§Œ¬æ§Œπ‘ŒÛ§À§Ë§ÎΩËÕ˝§«FWHT§Ú𑧶§À§œ°¢∆˛ŒœΩÁΩ¯§Œ∆˛§Ï¬ÿ§®§¨…¨Õ◊§»§ §Î°£ §¡§ §þ§À°¢DCT§‰DFT§»∞„§√§∆∑∏øÙ§¨1§´-1§«°¢§µ§È§À∑◊ªª§Œ∑¡§´§È°¢•–•ø•’•È•§±Èªª§œ§…§¡§È§´§Èπ‘§√§∆§‚ɬͧ §§§∑°¢ΩÁΩ¯§Ú•∑•„•√•’•Î§∑§∆§‚ɬͧ §§°£Wikipedia§ŒøÞ§À§œ±Û§§Ωͧ»§Œ±Èªª§´§È§Œ ˝À°§¨ Œ„º®§µ§Ï§∆§§§Î§¨°¢œ¿ ∏§À§Ë§√§∆§œŒŸ∆±ªŒ§Œ±Èªª§´§È§Œ ˝À°§‚º®§∑§∆§¢§Í°¢º¬¡ı槜ŒŸ∆±ªŒ§Œ±Èªª§´§È§Œ ˝§¨ ¨§´§Í§‰§π§§§»ª◊§¶°£

Discrete Walsh-Hadamard Transform (Œ•ª∂•¶•©•Î•∑•Â°¶•¢•¿•Þ°º•Î —¥π) - MATLAB & Simulink Example - MathWorks§ÚScilab§»Octave§«º¬π‘§∑§øŒ„°£ Matlab§»Scilab§œª˜§∆§§§Î§Ë§¶§«∫Ÿ§´§§¥ÿøÙ≈˘§À∏þ¥π¿≠§¨§ §Ø°¢∞’≥∞§À∂Ïœ´§π§Î§≥§»§¨¬ø§§°£Octave§À§œfwht()ifwht()§¨§¢§Î§¨Scilab§À§œ§ §§°£§≥§ŒMatlab§ŒŒ„§«§œ°¢ Octave§«§œ§€§Ðɬͧ §Ø∆∞§§§ø°£Scilab§À§œImage Processing Toolbox§¨§¢§Í°¢§≥§Œ√ʧÀWalsh transform§»Hadamard transform§¨∆˛§√§∆§§§Î§Œ§«°¢ §≥§Ï§Úª»§¶æÏπÁ§À§œ Ã≈”•§•Û•π•»°º•Î§¨…¨Õ◊§«§¢§Î°£
Walsh matrix§ŒΩÁΩ¯§Œ•”•√•»±Èªª§¨§Ô§´§Í§À§Ø§§§¨°¢•∞•Ï•§•≥°º•…§Œ•”•√•»µ’≈æ§∑§ø√Õ§«π‘ŒÛ§ŒŒÛ§Ú¿∞ŒÛ§µ§ª§∆§§§Î°£ •∞•Ï•§•≥°º•…§œ°¢±¶•∑•’•»§∑§ø√Õ§»§ŒXOR§¿§¨°¢≤ºµ≠§ŒŒ„§«§œ°¢¿Ë§À•”•√•»µ’≈æ§∑§∆§´§ÈXOR§∑§∆§§§Î°£
// Gray code function list = graycode(N) P=2^N; list = dec2bin(bitxor(int((0:P-1)/2),0:P-1))'; endfunction graycode(3) graycode(4)
--> graycode(3) ans = !000 ! ! ! !001 ! ! ! !011 ! ! ! !010 ! ! ! !110 ! ! ! !111 ! ! ! !101 ! ! ! !100 ! --> graycode(4) ans = !0000 ! ! ! !0001 ! ! ! !0011 ! ! ! !0010 ! ! ! !0110 ! ! ! !0111 ! ! ! !0101 ! ! ! !0100 ! ! ! !1100 ! ! ! !1101 ! ! ! !1111 ! ! ! !1110 ! ! ! !1010 ! ! ! !1011 ! ! ! !1001 ! ! ! !1000 !
% Gray code function list = graycode(N) P=2^N; list = dec2bin(bitxor(bitshift(0:P-1,-1),0:P-1)); end graycode(3) graycode(4)
>> graycode(3) ans = 000 001 011 010 110 111 101 100 >> graycode(4) ans = 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000
// Length of Walsh (Hadamard) functions N = 8; hadamardMatrix=hadamard(N) // Hadamard index HadIdx = 0:N-1; // Number of bits to represent the index M = log2(N)+1; //binHadIdx = fliplr(dec2bin(HadIdx,M))-'0'; //¥ÿøÙ flipdim(A,1) §œ flipud(A) §»∆±§∏ //¥ÿøÙ flipdim(A,2) §œ¥ÿøÙ fliplr(A) §»∆±§∏ // Bit reversing of the binary index binHadIdx = strrev(dec2bin(HadIdx(:),M)) // Pre-allocate memory binSeqVdx = zeros(N,M); for k = 1:1:N binSeqVdx(k,:) = strtod(strsplit(binHadIdx(k)))'; end // Pre-allocate memory binSeqIdx = zeros(N,M-1); //for k = M:-1:2 // binSeqIdx(:,k) = xor(binHadIdx(:,k),binHadIdx(:,k-1)); //end for k = M:-1:2 binSeqIdx(:,k) = bitxor(binSeqVdx(:,k),binSeqVdx(:,k-1)); end // Binary to integer sequency index //SeqIdx = binSeqIdx*(2^((M-1:-1:0)')); for k = 1:1:N // Binary sequency index HadIdx(k) = bin2dec(strcat(string(binSeqIdx(k,:)))); end // 1-based indexing walshMatrix = hadamardMatrix(HadIdx+1,:)
hadamardMatrix = 1. 1. 1. 1. 1. 1. 1. 1. 1. -1. 1. -1. 1. -1. 1. -1. 1. 1. -1. -1. 1. 1. -1. -1. 1. -1. -1. 1. 1. -1. -1. 1. 1. 1. 1. 1. -1. -1. -1. -1. 1. -1. 1. -1. -1. 1. -1. 1. 1. 1. -1. -1. -1. -1. 1. 1. 1. -1. -1. 1. -1. 1. 1. -1. walshMatrix = 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. -1. -1. -1. -1. 1. 1. -1. -1. -1. -1. 1. 1. 1. 1. -1. -1. 1. 1. -1. -1. 1. -1. -1. 1. 1. -1. -1. 1. 1. -1. -1. 1. -1. 1. 1. -1. 1. -1. 1. -1. -1. 1. -1. 1. 1. -1. 1. -1. 1. -1. 1. -1.
pkg load signal N = 8; % Length of Walsh (Hadamard) functions hadamardMatrix = hadamard(N) % Hadamard index HadIdx = 0:N-1; % Number of bits to represent the index M = log2(N)+1; % Bit reversing of the binary index binHadIdx = fliplr(dec2bin(HadIdx,M))-'0'; % Pre-allocate memory binSeqIdx = zeros(N,M-1); for k = M:-1:2 % Binary sequency index binSeqIdx(:,k) = xor(binHadIdx(:,k),binHadIdx(:,k-1)); end % Binary to integer sequency index SeqIdx = binSeqIdx*pow2((M-1:-1:0)'); % 1-based indexing walshMatrix = hadamardMatrix(SeqIdx+1,:)
hadamardMatrix = 1 1 1 1 1 1 1 1 1 -1 1 -1 1 -1 1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1 -1 -1 1 1 1 1 1 -1 -1 -1 -1 1 -1 1 -1 -1 1 -1 1 1 1 -1 -1 -1 -1 1 1 1 -1 -1 1 -1 1 1 -1 walshMatrix = 1 1 1 1 1 1 1 1 1 1 1 1 -1 -1 -1 -1 1 1 -1 -1 -1 -1 1 1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 1 -1 1 -1 -1 1 -1 1 1 -1 1 -1 1 -1 1 -1
N = 8; H = hadamard(N); x = 8.*H(1,:) + 12.*H(3,:) + 18.*H(5,:) + 10.*H(8,:); // fwht(x,8,'hadamard') y = x * hadamardMatrix / N // ifwht(y,8,'hadamard') z = y * hadamardMatrix norm(x-z)
y = 8. 0. 12. 0. 18. 0. 0. 10. z = 48. 28. 4. 24. -8. 12. -12. -32. ans = 0.
% Fast Walsh-Hadamard transform y1 = fwht(walshMatrix) N = 8; H = hadamard(N); x = 8.*H(1,:) + 12.*H(3,:) + 18.*H(5,:) + 10.*H(8,:); y = fwht(x,N,'hadamard') xHat = ifwht(y,N,'hadamard') norm(x-xHat)
y1 = 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 y = 8 0 12 0 18 0 0 10 xHat = 48 28 4 24 -8 12 -12 -32 ans = 0
Octave§Œ ˝§¨•”•√•»±Èªª≈˘§Œ¥ÿøÙ§¨ª»§§§‰§π§Ø°¢æµ≠§Œπ‘ŒÛΩÁ§Œ∆˛§Ï¬ÿ§®§œ§‚§¶æا∑¥ √±§À…Ωµ≠§«§≠§Î°£ Octave§«§œ°¢ªÿƒÍ§∑§ §±§Ï§–°¢fwht()§œsequency§¨µ¨ƒÍ§«§¢§Í°¢§≥§Ï§œMatlab§»∆±§∏∆∞∫Ó§«§¢§Î°£
HadIdx
HadIdx = 0. 4. 6. 2. 3. 7. 5. 1.
x = [19 -1 11 -9 -7 13 -15 5]; // y = fwht(x) y = x * walshMatrix / 8
y = 2. 3. 0. 4. 0. 0. 10. 0.
% Sequency (Walsh) Ordered Walsh-Hadamard Matrix pkg load signal N=8; bitand(bitxor(bitshift(bitrevorder(0:N-1),1),bitrevorder(0:N-1)),(N-1)) bitand(bitrevorder(bitxor(bitshift(0:N-1,1),0:N-1)),(N-1)) % Dyadic (Paley) ordered Matrix bitrevorder(0:N-1) paleyMatrix = hadamardMatrix(bitrevorder(0:N-1)+1,:) fwht(paleyMatrix,N,'dyadic')
>> bitand(bitxor(bitshift(bitrevorder(0:N-1),1),bitrevorder(0:N-1)),(N-1)) ans = 0 4 6 2 3 7 5 1 >> bitand(bitrevorder(bitxor(bitshift(0:N-1,1),0:N-1)),(N-1)) ans = 0 4 6 2 3 7 5 1 >> >> % Dyadic (Paley) ordered Matrix >> bitrevorder(0:N-1) ans = 0 4 2 6 1 5 3 7 >> >> paleyMatrix = hadamardMatrix(bitrevorder(0:N-1)+1,:) paleyMatrix = 1 1 1 1 1 1 1 1 1 1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 >> fwht(paleyMatrix,N,'dyadic') ans = 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1
x = [19 -1 11 -9 -7 13 -15 5]; y = fwht(x) z = fwht(x,8,'dyadic') p = x*paleyMatrix/8 porder = bitrevorder(0:N-1); fwht(x(porder+1),N,'hadamard') fwht(x,N,'hadamard')(porder+1)
>> y = fwht(x) y = 2 3 0 4 0 0 10 0 >> z = fwht(x,8,'dyadic') z = 2 3 4 0 0 10 0 0 >> p = x*paleyMatrix/8 p = 2 3 4 0 0 10 0 0 >> porder = bitrevorder(0:N-1); >> fwht(x(porder+1),N,'hadamard') ans = 2 3 4 0 0 10 0 0 >> fwht(x,N,'hadamard')(porder+1) ans = 2 3 4 0 0 10 0 0
•¢•¿•Þ°º•Î —¥π§¨¿π§Û§À∏¶µÊ§µ§Ï§∆§§§ø1970«Ø¬Â§ŒÀЧÚ∏°∫˜§π§Î§»°¢sequency orderedÕ—§Œπ‚¬Æ —¥πÀ°§‚ƒÛ∞∆§µ§Ï§∆§§§ø°£∫«∂·§Œº¬¡ı§Ú∏°∫˜§∑§ø§»§≥§Ì°¢MATLAB≈˘§ŒøÆπÊΩËÕ˝§Œ ¨ÃÓ§«§œæµ≠§Œ•–•ø•’•È•§±Èªª§»∆˛Ω–Œœ§Œ√÷¥π§Úº¬π‘§π§Î ˝À°§¨¬ø§´§√§ø§¨°¢ JuliaÕ—§ŒHadamard.jl•—•√•±°º•∏§«§œSequecy orderedÕ—§Œπ‚¬Æ•¢•Î•¥•Í•∫•ý§¨º¬¡ı§µ§Ï§∆§§§ø°£ Walsh Functions And Their Applications K Beauchamp by K. G. Beauchamp§»§§§¶1975«ØΩ–»«§ŒÀÐ (mirror)§À§œøÞ§Ú¥Þ§·§∆§´§ §ÍæЧ∑§ØΩ“§Ÿ§È§Ï§∆§™§Í°¢Fortran§À§Ë§Îº¬¡ı§‚∫Ч√§∆§§§Î§Œ§«∞Ï…Ù≈æ∫Чπ§Î°£ √¢§∑°¢OCR§À§Ë§Î∆…§þºË§Í§Œ§ø§·∞Ï…Ù∏Ìø¢§Œ≤ƒ«Ω¿≠§¨§¢§Î§Œ§»°¢∫«∂·§Œ•≥•Û•—•§•È§ÀƒÃ§∑§øæÏπÁ•®•È°º§¨Ω–§Î≤ƒ«Ω¿≠§¨§¢§Î°£
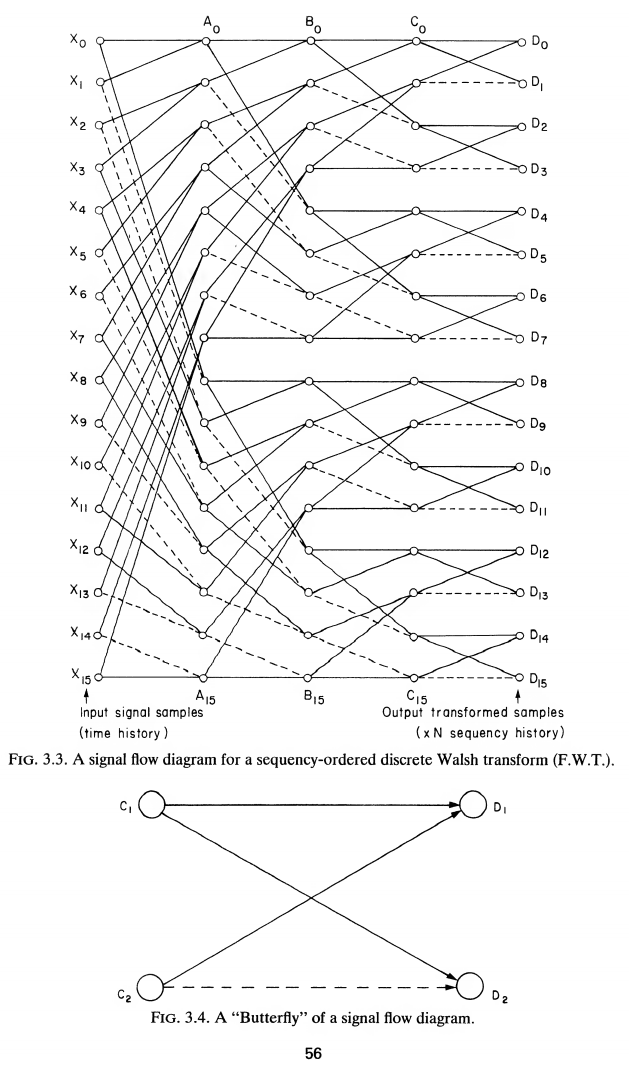
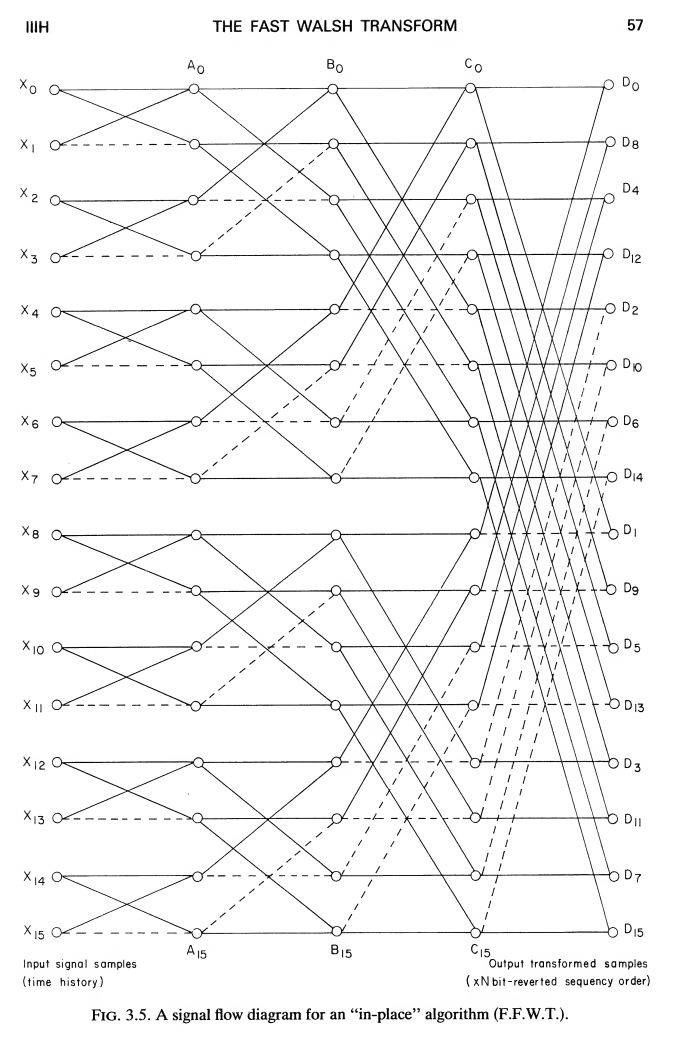
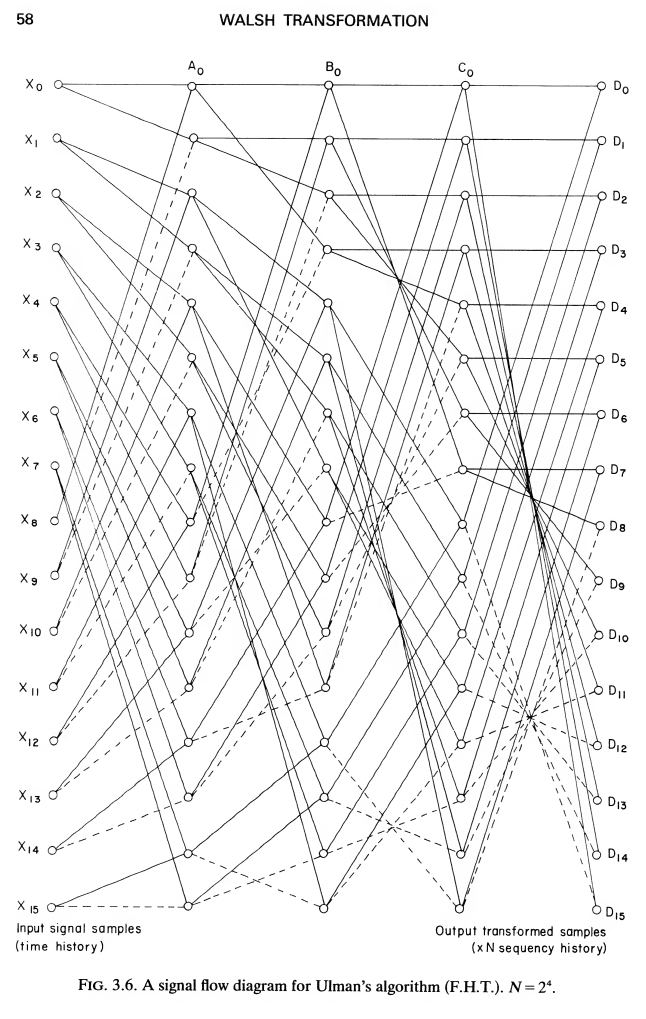
Appendix I A Signal processing computer programs 192 B Program summary 192 C Fast Walsh transform routines FWT and FFWT 193 D Fast Walsh transform routines FHT and FRT 195 C2 Calling sequence CALL FWT (N,X, WORK) or CALL FFWT (N,X) where N is an integer constant or variable and must be a power of 2. X is the name of a real array which on input contains the N data samples and on output contains the transformed signal. WORK is an array dimensioned N/2 and is used for temporary work space. SUBROUTINE FWT(N,X,Y) C THIS ROUTINES PERFORMS A FAST WALSH TRANSFORM ON AN INPUT SERIES X C LEAVING THE TRANSFORMED RESULTS IN X, THE ARRAY Y IS USED FOR WORKING C SPACE. X AND Y ARE DIMENSIONED N WHICH MUST BE A POWER OF 2 C THE RESULTS OF THIS WALSH TRANSFORM ARE IN SEQUENCY ORDER DIMENSION X(N) ,Y(N) N2=N/2 M=ALOG2 (FLOAT (N) ) DO 4 L=1,M NY=0 NZ=2** (L-1) NZI=2*NZ NZN=N/NZI DO 3 I=1, NZN NX=NY+1 NY=NY+NZ JS=(I-1) *NZI JD=JS+NZI+1 DO 1 J=NX,NY JS=JS+1 J2=J+N2 Y(JS)=X(J)+X(J2) JD= JD-1 Y ( JD) =ABS (X ( J) -X ( J2 ) ) 1 CONTINUE 3 CONTINUE CALL FMOVE (Y(1) ,X(1) ,N) 4 CONTINUE RETURN END SUBROUTINE FFWT(N,X) C THIS SUBROUTINES PERFORMS AN IN PLACE FAST WALSH TRANSFORM LEAVING THE C TRANSFORMED VALUES IN SEQUENCY ORDER AFTER BIT-REVERSAL DIMENSION X (N) ,INT (24) M=ALOG2 (FLOAT (N) ) DO 10 1=1, M 10 INT (I) =2** (M-l) DO 4 L=1,M NZ=2** (L-1) NZI=2*NZ NZN=N/NZI NZ2=NZ/2 IF (NZ2.EQ.0) NZ2=NZ2+1 DO 3 1=1, NZN JS=(I-1) *NZI Z=1.0 DO 2 11=1,2 DO 1 J=1,NZ2 JS=JS+1 J2=JS+NZ HOLD=X(JS) +Z*X(J2) Z=-Z X ( J2) =X(JS) +Z*X(J2) X ( JS) =HOLD Z=-Z 1 CONTINUE IF (L.EQ. 1) GO TO 3 Z=-1.0 2 CONTINUE 3 CONTINUE 4 CONTINUE C BIT-REVERSAL SECTION C THE TRANSFORMED ARRAY IS REARRANGED INTO SEQUENCY ORDER NW=0 DO 50 K = 1 , N C CHOOSE CORRECT INDEX & SWITCH ELEMENTS IF NOT ALREADY SWITCHED NW1=NW+1 IF (NW1-K) 55,55,60 60 HOLD=X (NW1 ) X(NW1)=X(K) X (K) =HOLD 55 CONTINUE C BUMP UP SERIES BY ONE DO 70 1=1, M II=I IF (NW.LT.INT (I) ) GO TO 80 MW=NW/INT(I) MWl=MW/2 IF (MW.GT.2*MW1) GO TO 70 GO TO 80 70 NW=NW- INT ( I ) 80 NW=NW+INT (II) 50 CONTINUE RETURN END
D Fast Walsh transform routines FHT and FRT The program FHT forms an alternative method to that of FWT described previously and is slightly faster. A signal flow diagram was given in Fig. 3.7 which indicated the arithmetic steps required for the transformation of a time series for N = 16 samples. Solid lines meeting at an intersection indicate addition, whereas dotted lines indicate subtraction. A disadvantage of the Walsh transform for some purposes is that it is not invariant to circular time shifts of the series being transformed. The particu- lar sequence of calculations, used in FHT, enables a slight modification to be carried out in order to obtain a transform, known as the R-transform (see Section III I) which is invariant to circular time shift. This modification involves the replacement of the subtractive terms obtained during the interim calculations by their absolute values. However, unlike the Walsh transform, the R-transform does not permit the original series to be recovered by a second transformation, i.e. it is not its own inverse. D.1 Program details The programs are written in FORTRAN for the ICL 1900 computer, using all single precision variables. Program length for the routines are 26 statements or 134 words. The data input and output is made via a calling sequence. A working space of N values is required. D2 Calling sequence CALL FHT (N,X,WORK) or CALL FRT (N,X,WORK) where N is an integer constant or variable and X and WORK are the names of real arrays holding N samples. WORK is used for temporary working space. X contains the input signal on entry to the routine and the transformed series is left in X in sequency order on return from the routine. SUBROUTINE FHT(N,X,Y) C THIS ROUTINES PERFORMS A FAST WALSH TRANSFORM ON AN INPUT SERIES X C LEAVING THE TRANSFORMED RESULTS IN X, THE ARRAY Y IS USED FOR WORKING C SPACE. X AND Y ARE DIMENSIONED N WHICH MUST BE A POWER OF 2 C THE RESULTS OF THIS HADAMARD TRANSFORM ARE IN SEQUENCY ORDER DIMENSION X(N),Y(N) N2=N/2 N=ALOG2(FLOAT (N) ) DO 4 L=1,M NY=0 NZ=2 ** (L-1) NZI=2*NZ NZN=N/NZI DO 3 I=1, NZN NX=NY+1 NY=NY+NZ JS=(I-1)*NZI JD=JS+NZI+1 DO 1 J=NX,NY JS=JS+1 J2=J+N2 Y(JS)=X(J)+X(J2) JD=JD-1 Y(JD)=X(J)-X(J2) 1 CONTINUE 3 CONTINUE CALL FMOVE(Y(1),X(1),N) 4 CONTINUE RETURN END D FAST WALSH TRANSFORM ROUTINES FHT AND FRT SUBROUTINE FRT(N,X,Y) C THIS ROUTINE PERFORMS A FASTER TRANSFORM ON AN INPUT SERIES X C LEAVING THE TRANSFORMED RESULTS IN X, THE ARRAY Y IS USED FOR WORKING C SPACE. X IS DIMENSIONED N AND Y N/2 , WHERE N MUST BE A POWER OF 2 C THE RESULTS OF THIS R TRANSFORM ARE IN SEQUENCY ORDER N2=N/2 DIMENSION X (N) ,Y(N2) M=ALOG2 (FLOAT (N) ) Z=-1.0 DO 4 J=l, M NL=2** (M-J+l) Jl=2** (J-l) DO 3 L=1 f Jl IS= (I-1) *N1+1 II=0 W=2 DO 1 I=IS,IS+N1-1,2 A=X(I) X (IS+Il) =A+X (I+1) II = II+1 Y (II) =(X(I+1) -A) *W W=W*Z 1 CONTINUE CALL FMOVE (Y ( 1 ) ,X(IS+Nl/2) ,Nl/2) 3 CONTINUE 4 CONTINUE RETURN END
Scilab§»Octave§«Natural order§»Sequency order§Œ•–•ø•’•È•§±Èªª§Úº¬¡ı§∑§∆§þ§Î°£Sequency order§Œ•–•ø•’•È•§±Èªª§«§œ°¢Natural order§«§Œ¿ËΩ“§Œ§Ë§¶§ ΩÁΩ¯•∑•„•√•’•Î§¨Õ¯§´§ §§§Œ§«√Ì∞’°£
fhtnat() 1D natural (Hadamard) ordered fast Hadamard transform
fhtseq() 1D sequency (Walsh) ordered fast Hadamard transform
≤ºµ≠§œScilab°¢Octave§ŒŒæ ˝§«ª»Õ—≤ƒ«Ω°£æÂΩ“§ŒƒÃ§Í°¢fhtnat()§Œ
for level=1:log2(N)
§œ
for level=log2(N):-1:1
§Œ§Ë§¶§Àµ’ΩÁ§«§‚≤ƒ°£
function data=fhtnat(data) N = length(data); tmp = zeros(1,N); level = 1; for level=1:log2(N) addbin = repmat([ones(1,2^(level-1)), zeros(1,2^(level-1))],1,2^(log2(N)-level)); addindex = find(addbin==1); subindex = find(addbin==0); tmp(addindex) = data(addindex) + data(subindex); tmp(subindex) = data(addindex) - data(subindex); data = tmp; end data = data/N; endfunction function data=fhtseq(data) N = length(data); tmp = zeros(1,N); addindex2 = find(repmat([1,0],1,N/2)==1); subindex2 = find(repmat([1,0],1,N/2)==0); for level=log2(N):-1:2 addbin = repmat([ones(1,2^(level-1)), zeros(1,2^(level-1))],1,2^(log2(N)-level)); addindex = find(addbin==1); subindex = find(addbin==0); decbin = repmat([1,0,0,1],1,N/4); addindexf = find(decbin==1); subindexf = find(decbin==0); tmp(addindex) = data(addindex2) + data(subindex2); tmp(subindex) = data(addindexf) - data(subindexf); data = tmp; end tmp(addindex2) = data(addindex2) + data(subindex2); tmp(subindex2) = data(addindex2) - data(subindex2); data = tmp; data = data/N; endfunction
pkg load signal; x = [19 -1 11 -9 -7 13 -15 5]; y = fwht(x,length(x),'hadamard') y = fhtnat(x) y = fwht(x,length(x),'sequency') y = fhtseq(x)
y = 2 0 4 0 3 10 0 0 y = 2 0 4 0 3 10 0 0 y = 2 3 0 4 0 0 10 0 y = 2 3 0 4 0 0 10 0
¬æ§Œsequency ordered fast Hadamard transform§Œº¬¡ı§Ú∏´§Î§»°¢æا∑ΩÁΩ¯§Ú —§®§ø ˝À°§¨Œ…§Øª»§Ô§Ï§∆§§§Î§Ë§¶§¿°£TVAL3 (TV minimization by Augmented Lagrangian and ALternating direction ALgorithms)§«º¬¡ı§µ§Ï§∆§§§Î ˝À°§»µ≠Ω“§µ§Ï§∆§§§Î§‚§Œ§¨¬ø§§§¨°¢æ§ŒFortran§Œ•≥°º•…§»∆±§∏ ˝À°§«§¢§Î°£ §‚§¡§Ì§Û°¢§≥§Œ ˝À°§‚ΩÁΩ¯§Úµ’§À§π§Î§≥§»§œ§«§≠§ §§°£
function data=fhtseqv2(data) N = length(data); tmp = zeros(1,N); addindex2 = find(repmat([1,0],1,N/2)==1); subindex2 = find(repmat([1,0],1,N/2)==0); tmp(addindex2) = data(addindex2) + data(subindex2); tmp(subindex2) = data(addindex2) - data(subindex2); data = tmp; addindexf = find(repmat([1,0,0,1],1,N/4)==1); subindexf = find(repmat([1,0,0,1],1,N/4)==0); for level=2:1:log2(N) vecbin = repmat([ones(1,2^(level-1)), zeros(1,2^(level-1))],1,2^(log2(N)-level)); addindex = find(vecbin==1); subindex = find(vecbin==0); tmp(addindexf) = data(addindex) + data(subindex); tmp(subindexf) = data(addindex) - data(subindex); data = tmp; end data = data/N; endfunction pkg load signal; x = [19 -1 11 -9 -7 13 -15 5]; y = fwht(x,length(x),'sequency') y = fhtseqv2(x)
y = 2 3 0 4 0 0 10 0 y = 2 3 0 4 0 0 10 0
Fast Walsh-Hadamard Transform in Python§´§È§Œ»¥øË°£
def FWHT(x): """ Fast Walsh-Hadamard Transform Based on mex function written by Chengbo Li@Rice Uni for his TVAL3 algorithm. His code is according to the K.G. Beauchamp's book -- Applications of Walsh and Related Functions. """ x = x.squeeze() N = x.size G = N/2 # Number of Groups M = 2 # Number of Members in Each Group # First stage y = np.zeros((N/2,2)) y[:,0] = x[0::2] + x[1::2] y[:,1] = x[0::2] - x[1::2] x = y.copy() # Second and further stage for nStage in xrange(2,int(log(N,2))+1): y = np.zeros((G/2,M*2)) y[0:G/2,0:M*2:4] = x[0:G:2,0:M:2] + x[1:G:2,0:M:2] y[0:G/2,1:M*2:4] = x[0:G:2,0:M:2] - x[1:G:2,0:M:2] y[0:G/2,2:M*2:4] = x[0:G:2,1:M:2] - x[1:G:2,1:M:2] y[0:G/2,3:M*2:4] = x[0:G:2,1:M:2] + x[1:G:2,1:M:2] x = y.copy() G = G/2 M = M*2 x = y[0,:] x = x.reshape((x.size,1)) return x/float(N)
TVAL3§´§È§Œ»¥øË°£
/*=================================================================
*
* \file fWHtrans.cpp
*
*
* This code computes the (real) fast discrete Walsh-Hadamard transform with sequency order according to the K.G. Beauchamp's book -- Applications of Walsh and Related Functions.
*
*
* This file is written by Chengbo Li from Computational and Applied Mathematics Department of Rice University.
*
*
* This is a MEX-file for MATLAB.
*
* 02/15/2010
*
*=================================================================*/
#include <math.h>
#include "mex.h"
#include "matrix.h"
//#include <stdio.h>
//#include <stdlib.h>
// #include <malloc.h>
// #include <stack>
//! Matlab entry function
/*!
* \param nlhs number of left-hand-side output arguments
* \param plhs mxArray of output arguments
* \param nrhs number of right-hand-side input arguments
* \param prhs mxArray of input arguments
*/
void mexFunction( int nlhs, mxArray *plhs[],
int nrhs, const mxArray*prhs[] )
{
int p, nStage, L, clm;
int i, j, m, n, N, J, K, M;
double *v_in, *v_out, *v_ext, *v_final, *temp;
/* Check for proper number of arguments */
if (nrhs != 1) {
mexErrMsgTxt("Only one input arguments required.");
}
else if (nlhs > 1) {
mexErrMsgTxt("Too many output arguments.");
}
/* Get the size and pointers to input data. */
m = mxGetM(prhs[0]);
n = mxGetN(prhs[0]);
/* Make sure that both input and output vectors have the length with 2^p where p is some integer. */
p = ceil(log2(m));
N = pow(2, p);
plhs[0] = mxCreateDoubleMatrix(N, n, mxREAL);
v_final = mxGetPr(plhs[0]);
v_in = mxGetPr(prhs[0]);
/* Extend the input vector if necessary. */
v_ext = (double*) mxCalloc(N, sizeof(double));
v_out = (double*) mxCalloc(N, sizeof(double));
for (clm=0; clm<n; clm++) {
/* C is row major while Matlab is column major */
for (j=0; j<m; j++){
v_ext[j] = (v_in+clm*m)[j];
}
for (j=m; j<N; j++){
v_ext[j] = 0;
}
for (i=0; i<N-1; i = i+2) {
v_ext[i] = v_ext[i] + v_ext[i+1];
v_ext[i+1] = v_ext[i] - v_ext[i+1] * 2;
}
L = 1;
/* main loop */
for (nStage = 2; nStage<=p; ++nStage){
M = pow(2, L);
J = 0;
K = 0; // difference between Matlab and C++
while (K<N-1){
for (j = J;j < J+M-1; j = j+2){
/* sequency order */
v_out[K] = v_ext[j] + v_ext[j+M];
v_out[K+1] = v_ext[j] - v_ext[j+M];
v_out[K+2] = v_ext[j+1] - v_ext[j+1+M];
v_out[K+3] = v_ext[j+1] + v_ext[j+1+M];
K = K+4;
}
J = J+2*M;
}
temp = v_ext;
v_ext = v_out;
v_out = temp;
L = L+1;
}
/* Perform scaling of coefficients. */
for ( i =0; i<N; ++i){
(v_final+clm*N)[i] = v_ext[i]/N;
}
}
/* Set free the memory. */
mxFree(v_out);
mxFree(v_ext);
return;
}
Python§«§‚π‘ŒÛ±Èªª§œ≤ƒ«Ω§«°¢Scilab§‰Octave§‰Matlab∞ ≥∞§À≤ø§´ª»§¶∏¿∏ϧ»§ §Î§»§Þ§∫µÛ§≤§È§Ï§Î°£Python 2§´§ÈPython 3§À§ §Í§´§ §Í —ππ≈¿§¨§¢§Î§¨°¢ •¢•¿•Þ°º•Î —¥π§Úº¬¡ı§∑§øŒ„§Ú≈æ∫Чπ§Î°£æµ≠§œPython 2Õ—§¿§√§ø§Œ§ÚPython 3Õ—§ÀΩÒ§≠ƒæ§∑§ø°£//§À§Ë§Î¿∞øÙΩ¸ªª§‰°¢xrange§Œ —¥π°¢print§Œ•÷•È•±•√•»§¨ºÁ§ —ππ≈¿§«§¢§Î°£
# -*- coding: utf-8 -*- """ Created on Thu Jun 11 15:21:43 2015 Fast Walsh-Hadamard Transform with Sequency Order Author: Ding Luo@Fraunhofer IOSB """ from math import log import numpy as np import GrayCode from time import clock def get_sequency_list(inputArray): """ Sort input 1D array into sequency order Utilizes gray code generation from a Python recipe from Internet. """ length = inputArray.size bitlength = int(log(length,2)) # Gray Code graycodes=GrayCode.GrayCode(bitlength) # Bitreverse of gray code bitreverse = [int(graycodes[i][::-1],2) for i in range(length)] outputArray = inputArray.copy() outputArray[bitreverse] = inputArray[:] return outputArray def SFWHT(X): """ 'Slower' Fast Walsh-Hadamard Transform Step#1 Get sequency-ordered input Step#2 Perform Hadamard Transform """ x=get_sequency_list(X) N = x.size M = int(log(N,2)) out = x.copy() for m in range(M): outtemp = out.copy() step = 2**m numCalc = 2**m for g in range(0,N,2*step): # number of groups for c in range(numCalc): index = g + c out[index] = outtemp[index] + outtemp[index+step] out[index+step] = outtemp[index] - outtemp[index+step] return out/float(N) def FWHT(x): """ Fast Walsh-Hadamard Transform Based on mex function written by Chengbo Li@Rice Uni for his TVAL3 algorithm. His code is according to the K.G. Beauchamp's book -- Applications of Walsh and Related Functions. """ x = x.squeeze() N = x.size G = N // 2 # Number of Groups M = 2 # Number of Members in Each Group # First stage y = np.zeros((G,2)) y[:,0] = x[0::2] + x[1::2] y[:,1] = x[0::2] - x[1::2] x = y.copy() # Second and further stage for nStage in range(2,int(log(N,2))+1): y = np.zeros((G//2,M*2)) y[0:G//2,0:M*2:4] = x[0:G:2,0:M:2] + x[1:G:2,0:M:2] y[0:G//2,1:M*2:4] = x[0:G:2,0:M:2] - x[1:G:2,0:M:2] y[0:G//2,2:M*2:4] = x[0:G:2,1:M:2] - x[1:G:2,1:M:2] y[0:G//2,3:M*2:4] = x[0:G:2,1:M:2] + x[1:G:2,1:M:2] x = y.copy() G = int(G/2) M = M*2 x = y[0,:] x = x.reshape((x.size,1)) return x/float(N) if __name__ == "__main__": x = np.random.random(1024**2) t1 = clock() y1 = SFWHT(x) t1 = clock() - t1 print(t1) t2 = clock() y2 = FWHT(x) t2 = clock() - t2 print(t2)
def isOdd(integer):
#assert isinstance(integer, int)
return integer % 2 == 1
def isEven(integer):
#assert isinstance(integer, int)
return integer % 2 == 0
def _list_to_string(li):
return ''.join(map(str, li))
class GrayCode(object):
def __init__(self, nbits):
self._nbits = nbits
self._grayCode = []
self.__generate()
def __getitem__(self, i):
return self._grayCode[i]
def __str__(self):
return str(self._grayCode)
__repr__ = __str__
def __iter__(self):
return self._grayCode.__iter__()
def __generate(self):
li = [0 for i in range(self._nbits)]
self._grayCode.append(_list_to_string(li))
for term in range(2, (1<<self._nbits)+1):
if isOdd(term):
for i in range(-1,-(self._nbits),-1):
if li[i]==1:
li[i-1]=li[i-1]^1
break
if isEven(term):
li[-1]=li[-1]^1
self._grayCode.append(_list_to_string(li))
class GrayCodeIterator(object):
def __init__(self, nbits):
self._nbits = nbits
def __iter__(self):
li = [0 for i in range(self._nbits)]
yield _list_to_string(li)
for term in range(2, (1<<self._nbits)+1):
if isOdd(term):
for i in range(-1,-(self._nbits),-1):
if li[i]==1:
li[i-1]=li[i-1]^1
break
if isEven(term):
li[-1]=li[-1]^1
yield _list_to_string(li)
if __name__=='__main__':
d = 4
codes=GrayCode(d)
print ('%d digits gray codes:', d)
print (codes)
print ('Using Iterator:')
#for c in GrayCode(20):
# print c
for c in GrayCodeIterator(20):
print (c)
import FWHT as fwht
import GrayCode as gc
import numpy as np
import importlib
importlib.reload(fwht)
importlib.reload(gc)
a = np.array([19, -1, 11, -9, -7, 13, -15, 5])
# Secuency ordered
print("Secuency ordered")
print(fwht.SFWHT(a))
print(fwht.FWHT(a).T)
from scipy.linalg import hadamard
print(hadamard(4, dtype=complex))
print(hadamard(8))
# Hadamard ordered
print(np.dot(a,hadamard(8))/8)
# // division error example
print("matrix indice")
print(a[0:8//2])
print(a[0:8/2])
print(np.zeros((8//2,2)))
np.zeros(8//2,2)
Secuency ordered
[ 2. 3. 0. 4. 0. 0. 10. 0.]
[[ 2. 3. 0. 4. 0. 0. 10. 0.]]
[[ 1.+0.j 1.+0.j 1.+0.j 1.+0.j]
[ 1.+0.j -1.-0.j 1.+0.j -1.-0.j]
[ 1.+0.j 1.+0.j -1.-0.j -1.-0.j]
[ 1.+0.j -1.-0.j -1.-0.j 1.+0.j]]
[[ 1 1 1 1 1 1 1 1]
[ 1 -1 1 -1 1 -1 1 -1]
[ 1 1 -1 -1 1 1 -1 -1]
[ 1 -1 -1 1 1 -1 -1 1]
[ 1 1 1 1 -1 -1 -1 -1]
[ 1 -1 1 -1 -1 1 -1 1]
[ 1 1 -1 -1 -1 -1 1 1]
[ 1 -1 -1 1 -1 1 1 -1]]
[ 2. 0. 4. 0. 3. 10. 0. 0.]
matrix indice
[19 -1 11 -9]
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-194-830b68925cc9> in <module>()
22 print("matrix indice")
23 print(a[0:8//2])
---> 24 print(a[0:8/2])
TypeError: slice indices must be integers or None or have an __index__ method
print(np.zeros((8//2,2))) np.zeros(8//2,2) np.zeros(8/2,2)
[[ 0. 0.] [ 0. 0.] [ 0. 0.] [ 0. 0.]] --------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-205-d3ad594fc4dc> in <module>() 1 print(np.zeros((8//2,2))) ----> 2 np.zeros(8//2,2) TypeError: data type not understood --------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-206-805c1441d66f> in <module>() ----> 1 np.zeros(8/2,2) TypeError: 'float' object cannot be interpreted as an integer
Matlab§À§œ°¢imread§‰imwrite§¨¡ı»˜§µ§Ï§∆§§§Î§¨°¢Scilab§«§œ…∏Ωýæı¬÷§«ª»§®§ §§°£6.0.x§«§œ Image Processing and Computer Vision (IPCV) Toolbox§Ú∆≥∆˛§π§Î§»ª»§®§Î§Ë§¶§À§ §Î°£ 5.x∑œ§«§œ çŒToolbox(Image_Processing_Toolbox_2 (IPT2) for 5.3.x°¢ Scilab Image and Video Processing (SIVP) toolbox for 5.5.x) §¨¬∏∫þ§∑°¢•–°º•∏•Á•Û§À§Ë§√§∆ª»§®§ÎToolbox§¨∞€§ §Î§Œ§œScilab§Œ∑Á≈¿§Œ∞ϧƒ§«§¢§Î°£
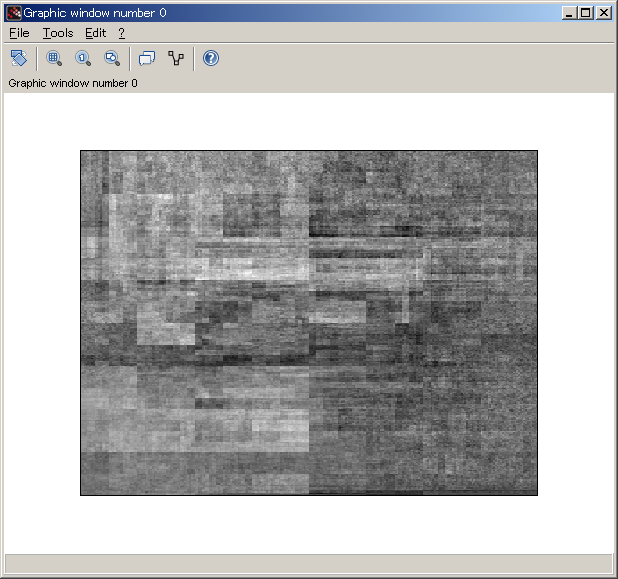
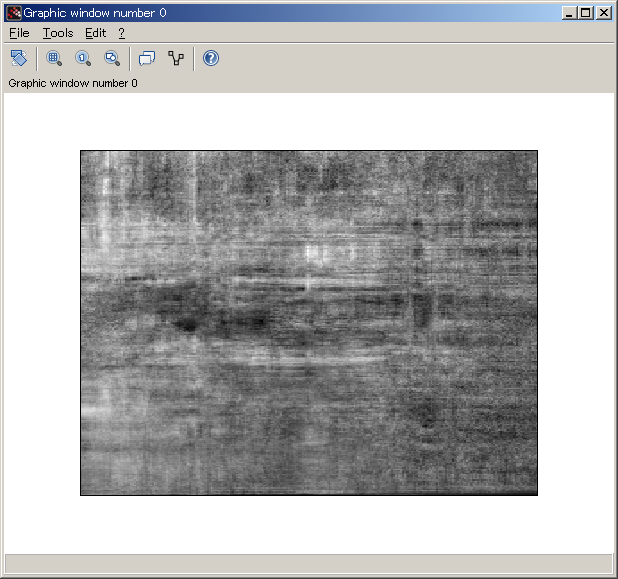
§Þ§∫§œHadamard matrix§Ú≤Ë¡¸§ÀΩÒ§≠Ω–§π§Œ§»°¢≤Ë¡¸§Ú∆…§þπ˛§Û§«∆Ûº°∏µŒ•ª∂•≥•µ•§•Û —¥π§Úπ‘§√§ø∑Î≤Ã§Ú…Ωº®§π§Î§»§≥§Ì§Þ§«°£∏∂≈¿…’∂·§À¬Á§≠§ √Õ§¨Ω∏§Þ§√§∆§§§Î§Œ§¨§Ë§Ø§Ô§´§Î°£
atomsInstall("IPCV")
N=256;
hadamardMatrix=hadamard(N);
function wmat=had2wal(hmat,msize)
HadIdx = 0:msize-1;
M = log2(msize)+1;
binHadIdx = strrev(dec2bin(HadIdx(:),M));
binSeqVdx = zeros(msize,M);
for k = 1:1:msize
binSeqVdx(k,:) = strtod(strsplit(binHadIdx(k)))';
end
binSeqIdx = zeros(msize,M-1);
for k = M:-1:2
binSeqIdx(:,k) = bitxor(binSeqVdx(:,k),binSeqVdx(:,k-1));
end
for k = 1:1:msize
HadIdx(k) = bin2dec(strcat(string(binSeqIdx(k,:))));
end
wmat = hmat(HadIdx+1,:);
endfunction
walshMatrix = had2wal(hadamardMatrix,N);
imwrite(hadamardMatrix,"hmat.bmp");
imwrite(walshMatrix,"wmat.bmp");
img_orig = double(imread("BRIDGE.bmp"));
imshow(uint8(img_orig));
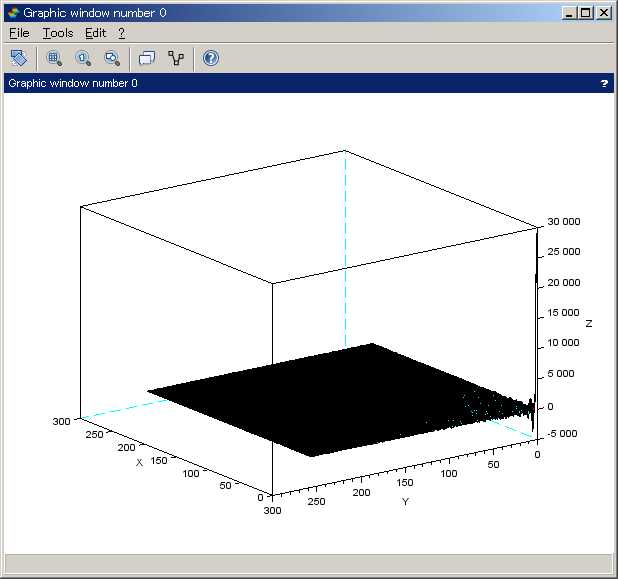
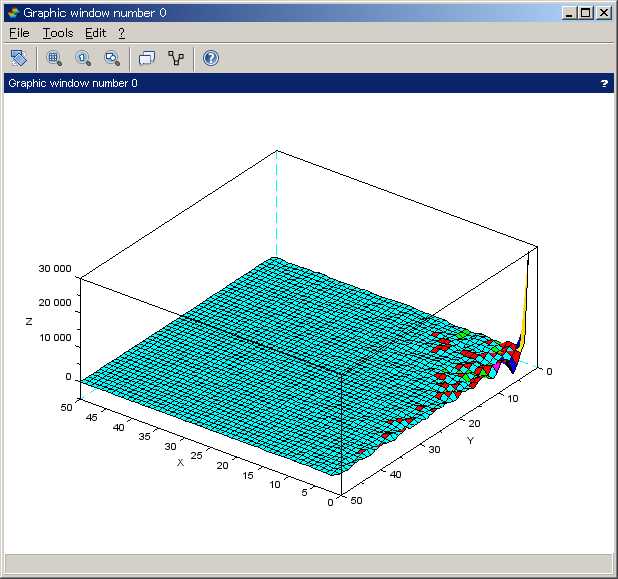
surf(imdct(img_orig))
surf(imdct(img_orig)(1:50,1:50))
hmat.bmp
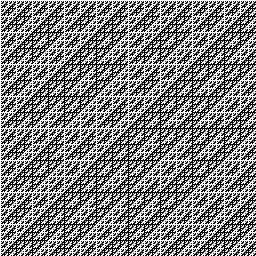
wmat.bmp

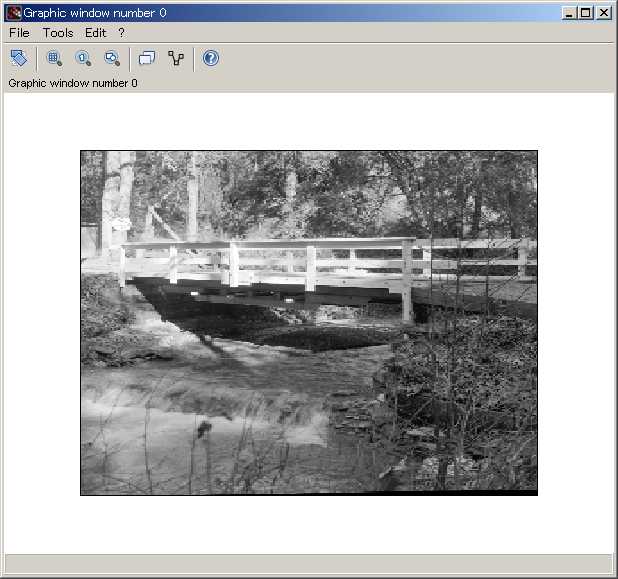
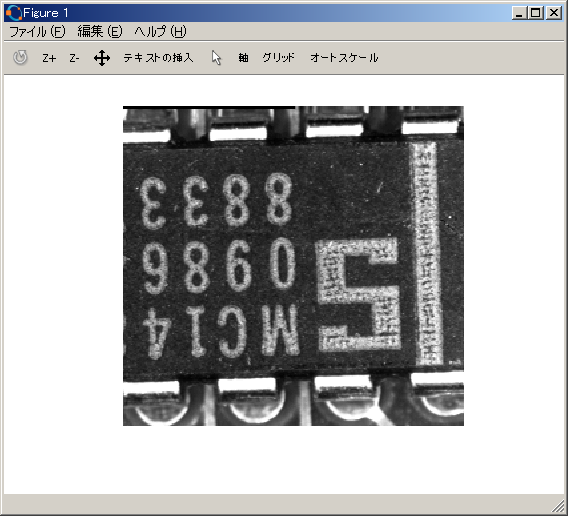
img_orig = double(imread("Text.bmp"));
imshow(uint8(img_orig));
img_dct = dct2(img_orig);
surf(img_dct);
surf(img_dct(1:50,1:50));
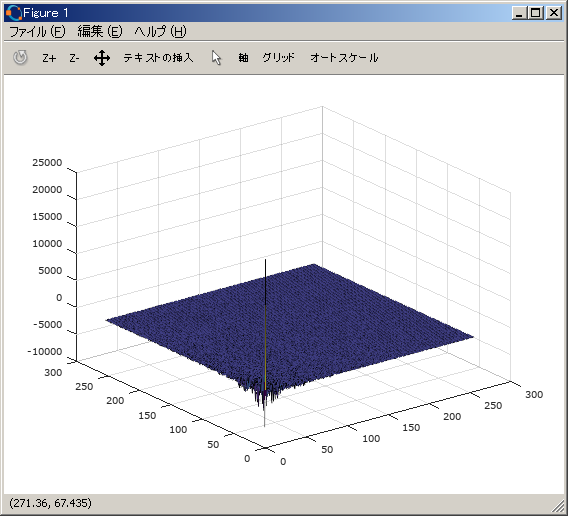
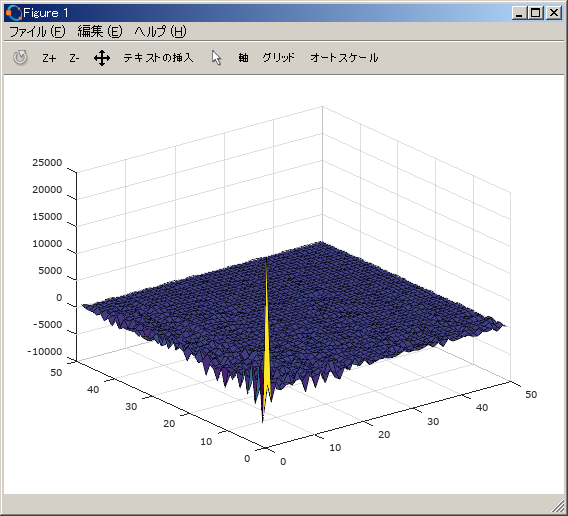
∆Ûº°∏µFFT§‰∆Ûº°∏µDCT§»∆±ÕÕ°¢π‘µ⁄§”ŒÛ§Ω§Ï§æ§Ï§Œ£≤≤Ûƒæ∏Ú —¥π§π§Ï§–§Ë§§°£ƒ„º˛«»§´§Èπ‚º˛«»§ÀΩÁ§À ¬§Ÿ§È§Ï§ø∑∏øÙ§Ú∆¿§Î§À§œ°¢Sequency Matrix§Úª»§¶§¨°¢ §Ω§Œ¬æ§Œπ‘ŒÛ§Úª»§√§∆§‚Œ…§§°£π‚¬Æ•¢•¿•Þ°º•Î —¥π§Œ§ø§·§À§œ°¢Natural order∞ ≥∞§«§œ°¢æÂΩ“§ŒƒÃ§Í∆˛ŒœΩÁ§Œ∆˛§Ï¬ÿ§®§¨…¨Õ◊§«§¢§Î°£
•¢•¿•Þ°º•Î —¥π§»Œ•ª∂•≥•µ•§•Û —¥π§œ°¢∑◊øÙπ‘ŒÛ∑¡§¨»Ê≥”≈™ª˜§∆§§§Î§¿§±§¿§¨°¢Õ∑§”§«µ’ —¥π§Ú§Ω§Ï§æ§Ï∆˛§Ï¬ÿ§®§ø¥ƒÏ§Úª»§¶§»°¢¡∞±“∑ðΩ—§Œ§Ë§¶§ ≤Ë¡¸§¨Ω–§Î°£
function imat = fwht2d(imat,hmat) N = sqrt(length(imat)) tmat = zeros(N,N); for i = 1:N tmat(i,:) = imat(i,:) * hmat / N; end imat = zeros(N,N); for j = 1:N imat(:,j) = hmat * tmat(:,j) end endfunction a2d = matrix(1:64,8,8)' // Sequency order fwht2d(a2d,walshMatrix) walshMatrix*a2d*walshMatrix / 8
a2d = 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. 61. 62. 63. 64. ans = 260. -16. 0. -8. 0. 0. 0. -4. -128. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -64. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -32. 0. 0. 0. 0. 0. 0. 0. ans = 260. -16. 0. -8. 0. 0. 0. -4. -128. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -64. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -32. 0. 0. 0. 0. 0. 0. 0.
// ƒÃæÔ§œ∞’㧌§ §§π‘∞Ÿ img_dct = imdct(img_orig); img_wal = fwht2d(img_dct,walshMatrix); imshow(uint8( (img_wal-min(img_wal))/(max(img_wal)-min(img_wal))*255 )); img_mat = fwht2d(img_orig,walshMatrix); img_ict = imidct(img_mat); imshow(uint8( (img_ict-min(img_ict))/(max(img_ict)-min(img_ict))*255 ));
Reader, suppose you were an idiot. And suppose you were a member of
Congress. But I repeat myself.
-- Mark Twain
Monica [on the phone]: Hey, have you guys eaten, because uh, Richard and I
just finished and we've got leftovers… Chicken and potatoes… What am I
wearing?… Actually, nothing but rubber gloves.
[Chandler and Joey come sprinting in]
Joey: Ya know, one of these times you're gonna really be naked and we're not
gonna come over.
-- David Crane & Marta Kauffman
-- "Friends" (T.V. Show) ( http://en.wikipedia.org/wiki/Friends )